ГДЗ Математика 6 клас. Підручник частина 2 [Мерзляк А., Полонський В., Якір М.] 2023
18.07.2024,
81,
0
31. Порівняння чисел
890. Чи є правильною нерівність:891. Порівняйте числа:
892. Порівняйте числа:893. Чи існує: 1) найменше натуральне число; 2) найбільше натуральне число; 3) найбільше від'ємне ціле число; 4) найбільше від'ємне число; 5) найменше від'ємне ціле число; 6) найбільше ціле число; 7) найменше ціле число; 8) найбільше недодатне число.
894. Розташуйте в порядку спадання числа:895. У порядку зростання числа: –11 В; –6 Я; –5,9 З; –4,1 О; –4,01 В; 0 С; 0,5 Ь; 4,5 К; 5,3 А.
896. Розташуйте в таблиці вказані речовини в порядку зростання їхніх температур кипіння.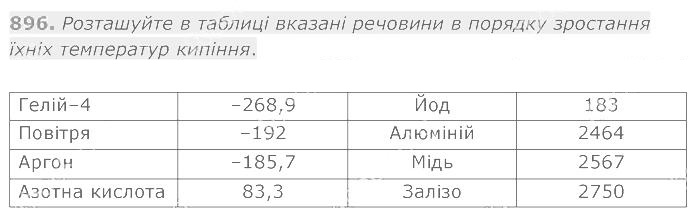
897. Чи існує таке значення х, при якому є правильною нерівність :898. Запишіть у вигляді нерівності твердження: 1) 9 > 0; 2) -20 < 0; 3) -6 < 0; 4) m < 0; 5) n > 0; 6) с > 0.
899. Знайдіть усі цілі значення х, при яки х є правильною нерівність: 1) -5, 3 < х < 2, 5: -5; -4; -3; -2; -1; 0; 1; 2. 2) -3 , 6 < х < 4: -3; -2; -1; 0; 1; 2; 3; 4. 3) -43 < х < -38: -42; -41; -40; -39; -38. 4) -274, 6 < х < -270, 8: -274; -273; -272; -271.900. Знайдіть усі цілі значення х, при яких Є правильною нерівність: 1) -5, 6 < х < 2: -5; -4; -3; -2; -1; 0; 1; 2. 2) -0, 61 < х < 4: 0; 1; 2; 3. 3) |х| < 0: 0.
901. Знайдіть найменше ціле число, при якому є правильною нерівність: 1) -9 < х < 3; х = -8. 2) х > -10; х = -10. 3) х > -2, 6; х = -2.902. Знайдіть найбільше ціле число, при якому є правильною нерівність: 1) -5 < х < 5, 6; х = 5. 2) х < -13; х = -12. 3) х < -64, 3; х = -64.
903. Між якими сусідніми цілими числами розташоване на кординатній прямій число:904. Запишіть три послідовних цілих числа, менше 3 яких дорівнює: 1) 3; 2) -4; 3) -2.
905. Запишіть чотири послідовних цілих числа, більше з яких дорівнює: 1) -8; 2) 0; 3) 3.
906. Чи може число бути меншим від 5, а його модуль — більшим за 5?
907. Яку цифру можна поставити замість зірочки, щоб утворилася правильна нерівність (розгляньте всі можливі випадки) :908. Яку цифру можна поставити замість зірочки, щоб утворилася правильна нерівність (розгляньте всі можливі випадки) :
909. При яких значеннях х є правильною нерівність |х| > х?910. Чи існує таке значення х, при якому є правильною нерівність:
911. На координатній прямій позначили числа a, b, m і п (рис. 98). Порівняйте:912. На якому з рисунків 99 (а - ґ) зображено числа а і b такі, що:
913. Чи правильне твердження. 1) якщо а > 3, то а — додатне число; 2) якщо b < 1, то b — від'ємне число; 3) якщо с > -1, то с — додатне число; 4) якщо d < -2, то d — від'ємне число;.
914. На координатній прямій (рис. 100) точками А, В, С і D позначили числа -0, 305; 0, 03; 0, 009 і -0, 053. Яка точка зображує число: 1) 0, 03; 2) -0, 305; 3) -0, 053?915. На координатній прямій (рис. 101) точками А, В, С і D позначили числа -1, 3; -0, 908; -1, 08 і -0, 76. Яка точка зображує число: 1) -0, 908; 2) -1, 08; 3) -0, 76?
916. Знайдіть усі цілі значення х, при яких є правильними одночасно обидві подвійні нерівності:917. Порівняйте числа - а і b, якщо:
918. У записах чисел стерли кілька цифр і замість них поставили зірочки. Порівняйте ці числа:919. У записах чисел стерли кілька цифр і замість них поставили Зірочки. Порівняйте ці числа:
920. Знайдіть два числа, кожне з яких більше за -5/17, але менше від -4/11921. Знайдіть два числа, кожне з яких більше за -7/17, але менше від -6/17
922. Чи правильне твердження:923. Порівняйте: 1) а і -а; 2) |а| і а; 3) |а| і -а.
924. За допомогою запису [а] позначають найбільше ціле число, яке не більше за а. Наприклад, [3, 2] = 3. Знайдіть:925. Використовуючи сторону рівностороннього трикутника як діаметр, побудували півколо (рис. 102). Чому дорівнює довжина пурпурової лінії, якщо сторона трикутника дорівнює 6 см?
926. Середній зріст десяти баскетболістів дорівнює 200 см, а середній зріст шести з них становить 190 см. Чому дорівнює середній зріст решти чотирьох баскетболістів?
927. Знайдіть значення виразу: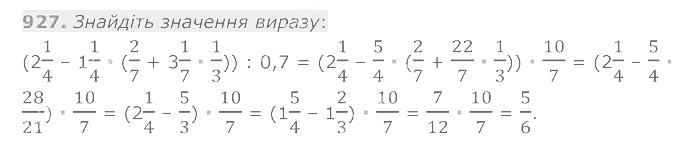 
928. Яке число має бути записане на координатній прямій у тому місці, куди вказує стрілка (рис. 103)?929. Яке число має бути записане на координатній прямій у тому місці, де бере початок стрілка (рис. 104)?
930. Є кілька колод завдовжки 4 м і 5 м, загальна довжина яких дорівнює 45 м. Яку найбільшу кількість розпилів потрібно зробити, щоб розпиляти всі колоди на чурбаки завдовжки їм? (Кожним розпилом розрізається тільки одна колода.)
Назад
ГДЗ Підручник Математика Частина 2 2023 Мерзляк Полонський Якір Гімназія НУШ 6 клас
Якщо помітили в тексті помилку, виділіть її та натисніть Ctrl + Enter
![ГДЗ Природознавство 5 клас. Підручник [Ярошенко О.Г., Бойко В.М.] 2018](/uploads/posts/2019-04/1555779316_5_p_y_u2018.jpg "ГДЗ Природознавство 5 клас. Підручник [Ярошенко О.Г., Бойко В.М.] 2018")
![ГДЗ Основи правознавства 9 клас. Підручник [Наровлянський О. Д.] 2017](/uploads/posts/2019-02/1550928122_9k_p_n_2017.jpg "ГДЗ Основи правознавства 9 клас. Підручник [Наровлянський О. Д.] 2017")
![ГДЗ Українська мова 8 клас. Підручник [Глазова О.П.] 2021](/uploads/posts/2021-10/1633720388_8k_y_g_2021.jpg "ГДЗ Українська мова 8 клас. Підручник [Глазова О.П.] 2021")
![ГДЗ Вступ до історії 5 клас. Підручник [Гісем О.В.] 2018](/uploads/posts/2019-07/1564163269_5k_i_h_2018.jpg "ГДЗ Вступ до історії 5 клас. Підручник [Гісем О.В.] 2018")