ГДЗ Математика 6 клас. Підручник частина 2 [Мерзляк А., Полонський В., Якір М.] 2023
18.07.2024,
81,
0
44. Графіки
1255. На рисунку 161 зображено графік зміни температури повітря протягом доби. 
1256. На рисунку 162 зображено графік зміни температури повітря протягом доби.
1257. На рисунку 163 зображено графік зміни температури розчину під час хімічного досліду.
1258. Мотоцикліст виїхав з дому й через деякий час повернувся назад. У дорозі він двічі зупинявся для відпочинку. На рисунку 164 зображено графік зміни відстані мотоцикліста від дому залежно від часу (графік руху мотоцикліста).
1259. На рисунку 165 зображено графік руху туристки.
1260. У таблиці наведено результати вимірювання температури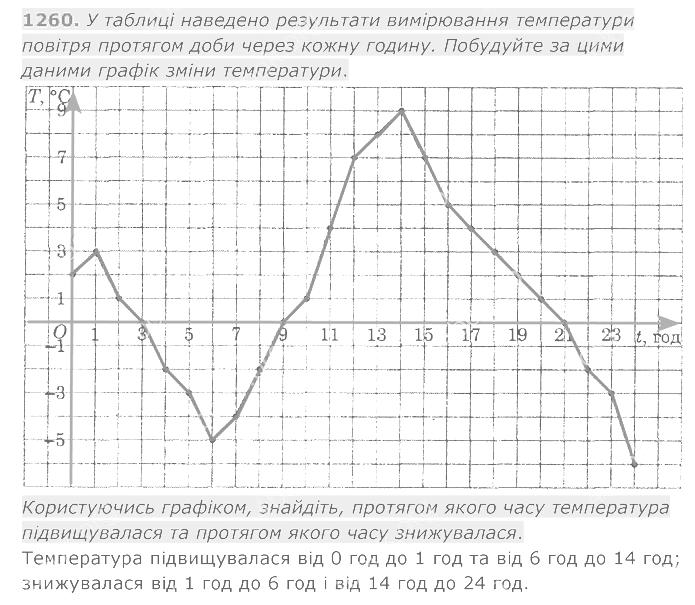
1261. Велосипедист виїхав із дому на прогулянку. Спочатку він їхав 2 год зі швидкістю 12 км/год, потім відпочив годину і повернувся додому зі швидкістю 8 км/год. 
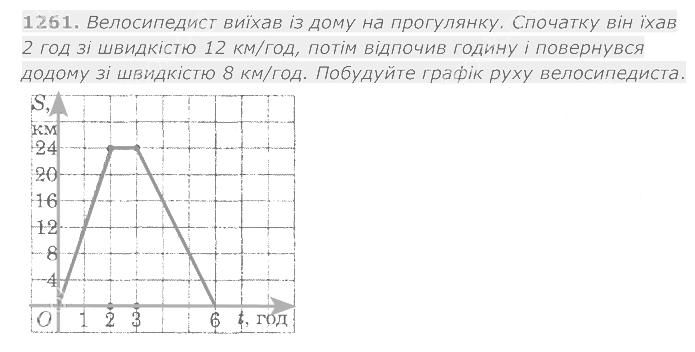1262. Побудуйте графік залежності змінної у від змінної у, яку задано формулою у = -2х.
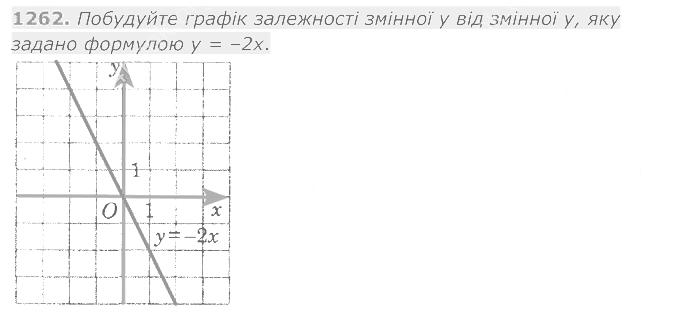1263. Побудуйте графік залежності змінної у від змінної х, яку задано формулою у = 3х.
1264. Листоноша має З різних конверти і 4 різних поштових марки. Скільки в нього є варіантів вибору конверта з маркою?
1265. Василько прочитав 24% сторінок книжки, а потім ще 7/15 сторінок книжки. Після цього йому залишилося прочитати 44 сторінки. Скільки сторінок у книжці?
1266. Знайдіть значення виразу: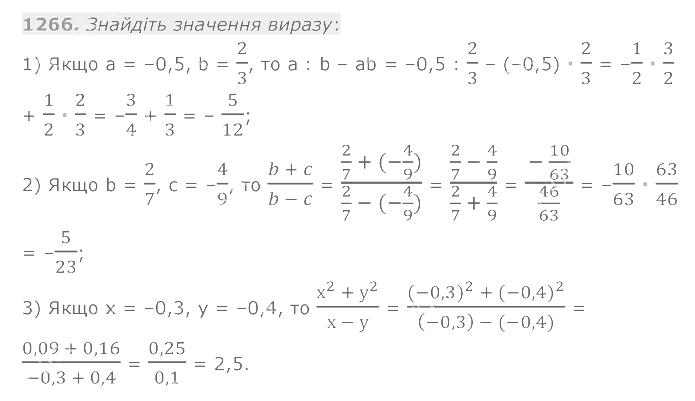
1267. У кожну клітинку квадрата розміром 6 х 6 клітинок записали одне з чисел –1, 0, 1. Чи можуть суми чисел, які записані в кожному рядку, у кожному стовпчику і по двох великих діагоналях, бути різними?
1268. Знайдіть значення виразу.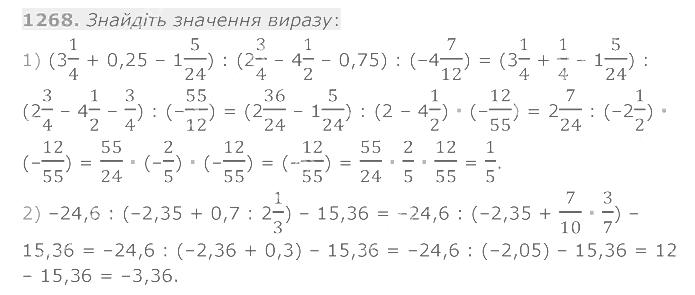
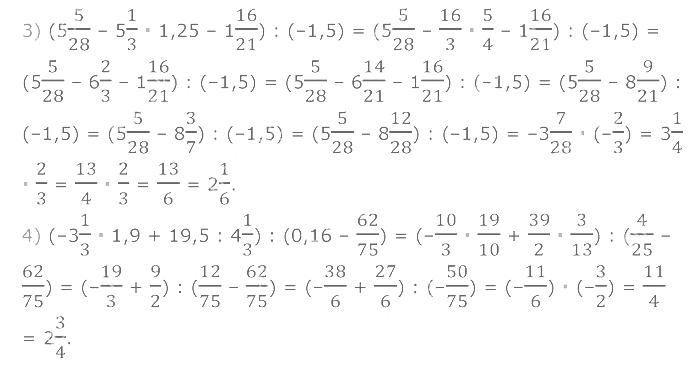
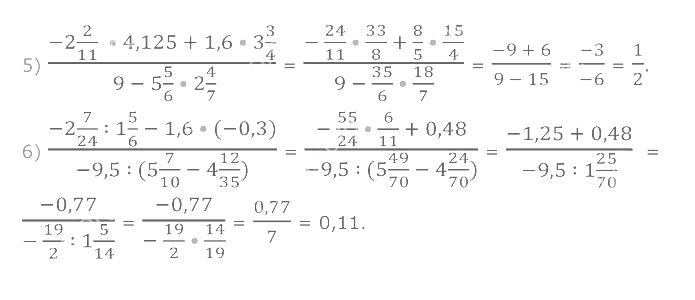
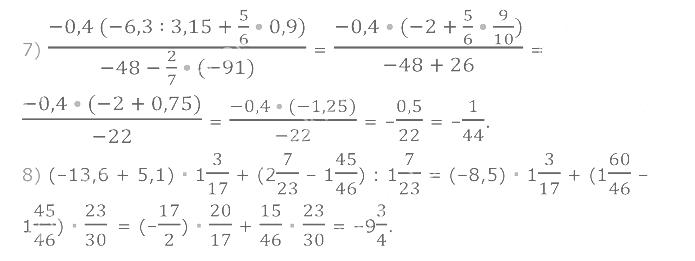1269. 1) Знайдіть 40 % від значення виразу
1270. 1) Знайдіть число, 28 % якого дорівнюють значенню виразу.
1271. 1) Знайдіть, скільки відсотків значення виразу становить від значення виразу. 2) Знайдіть, скільки відсотків значення виразу становить від значення виразу.
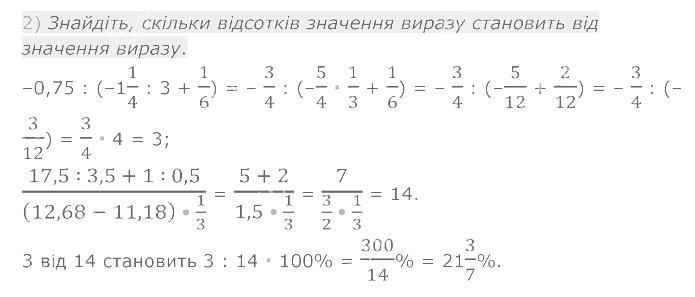1272. Яке із чисел а, b, с і d найменше, якщо:
1273. Яке із чисел |а|, |b|, |с| і |d| найбільше, якщо:
1274. Дано числа а і Ь. За якої умови: 1) а + b > а; 2) а + b < а; 3) а + b = а; 4) а + b = О?1275. Спростіть вираз:
1276. Спростіть вираз і знайдіть його значення:
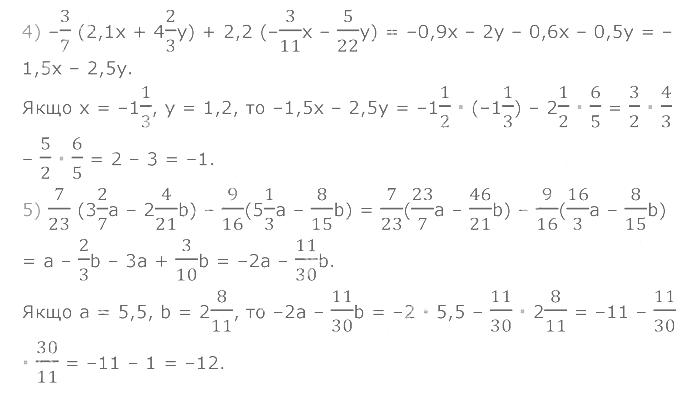1277. Розв'яжіть рівняння: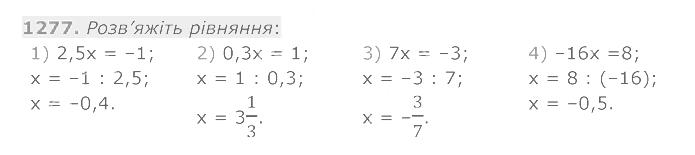
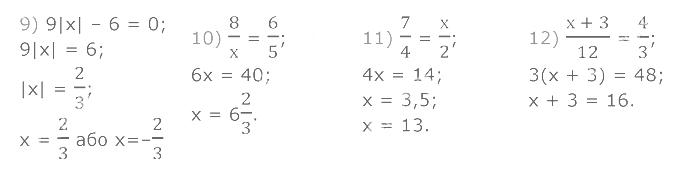
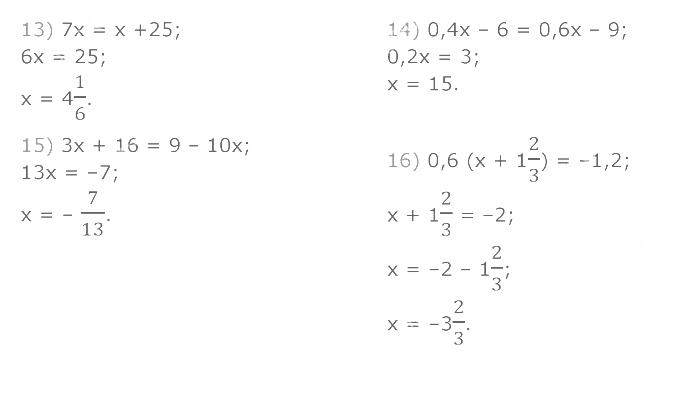
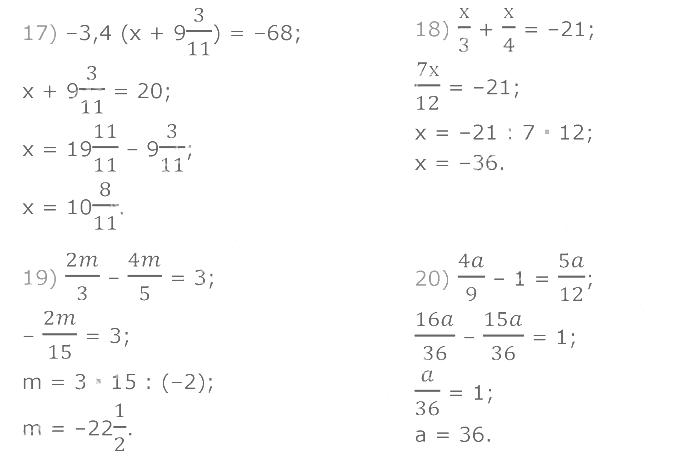
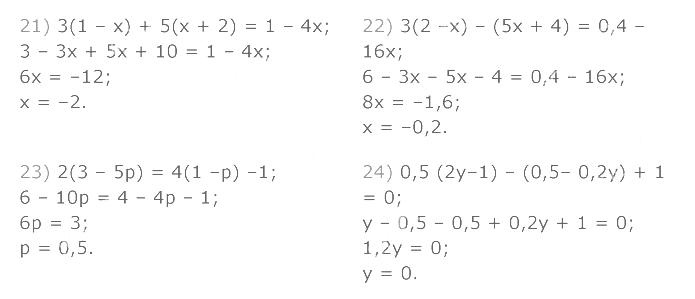
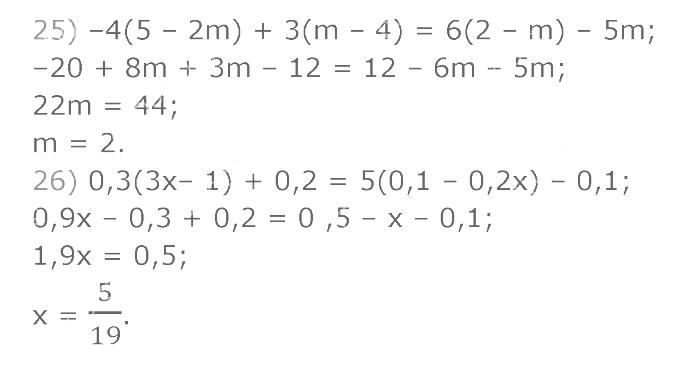1278. Замість зірочок поставте такі цифри, щоб виконувалася рівність:
1279. 1) Чому дорівнює найменший спільний дільник будь-якої пари натуральних чисел? 1. 2) Найбільший спільний дільник чисел а і b дорівнює а. Чи правильно, що число b кратне числу а? 3) Найменше спільне кратне чисел а і b дорівнює а. Чи правильно, що число b кратне числу а?
1280. Довжина кімнати дорівнює 725 см, а ширина — 375 см.
1281. Михайлик підрахував, що кількість оцінок «12» становить 7/18 усіх оцінок, отриманих ним за чверть, а кількість оцінок «9» — 7/12 усіх оцінок. Скільки всього оцінок отримав Михайлик за чверть, якщо відомо, що їх було більше за 50, але менше від 80?
1282. Басили на намагалася розкласти горіхи на рівні купки, але щоразу, коли вона розкладала їх по 4, по 5 або по 6, один горіх залишався зайвим. Скільки горіхів було у Василини, якщо відомо, що їх було менше ніж 100?
1283. Розташуйте числа.
1284. Маса глухаря дорівнює 3 кг 200 г і становить 2/5 маси лебедя. Маса чайки тановить 3/32 маси лебедя і 3/5 маси качки. Обчисліть масу кожного птаха.
1285. Робін-Бобін з’їв на обід 180 вареників із м’ясом, картоплею і вишнею. Вареники з картоплею становили 7/20 усіх вареників, або 9/14 вареників з вишнею. Скільки вареників з вишнею з’їв РобінБобін?
1286. У Кози-дерези було 42 кг капусти. На сніданок вона та семеро її козенят з’їли 2/7 усієї капусти, на обід — 40 % решти, а на вечерю — 5/6 того, що залишилося після сніданку й обіду. Скільки кілограмів капусти залишилося після цього у Кози-дерези?
1287. Наталка виконувала домашні завдання з математики, української мови та історії. Завдання з математики вона робила 1 1/3 год, що становило 8/15 усього часу, витраченого нею на виконання завдань. Завдання з української мови Наталка виконувала на 7/15 год довше, ніж з історії. Скільки часу вона виконувала завдання з української мови?
1287. Козак Іван Сірошапка три дні їхав верхи із села Вишневе у Запорозьку Січ. Першого дня він проїхав 7/19 шляху, другого — 55 % шляху, що залишився, а третього — решту 108 км. Яку відстань подолав Іван за три дні?
1289. Перша мотоциклістка проїжджає відстань між двома містами за 5 год, а друга — за час, в 1,4 раза більший, ніж перша. Хто з них проїде більшу відстань: перша за 3 год чи друга за 4 год?
1290. Порадьте Алісі в Країні Див, як їй відрізати пів метра від мотузки завдовжки 2/3 м, бо лінійку вона забула вдома.
1291. Фермерка заготувала сіно, якого може вистачити корові на 60 днів, а коневі — на 40 днів. За скільки днів корова і кінь разом з’їдять цей запас сіна?
1292. До басейну підведено три труби. Через першу трубу басейн наповнюється водою за 1 год, через другу — за 2 год, а через третю — за 3 год. За скільки хвилин наповниться басейн, якщо відкрити одночасно всі три труби?
1293. Ява Рень може скопати город за 12 год, а Павлуша Завгородній — за час, у 1,5 раза менший. За який час Ява та Павлуша скопають разом 5/8 городу?
1294. Через одну трубу басейн можна наповнити водою за 7 год, а через другу спорожнити за 8 год. За скільки годин наповниться басейн, якщо одночасно відкрити обидві труби?
1295. Перший робітник може розвантажити автомобіль з борошном за 6 год, а другий — за 4 год. Перший робітник пропрацював 2 год, а потім йому на допомогу прийшов другий. За скільки годин було розвантажено автомобіль?
1296. Ґава та Лисиця можуть з'їсти разом казан ковбаси за 8 хв. За скільки хвилин може з'їсти її Лисиця, якщо Ґава може це зробити за 18 хв?
1297. із двох міст одночасно назустріч один одному виїхали два велосипедисти й зустрілися через 3 1/5 год після виїзду. Один з них проїжджає відстань між містами за 5 1/3 год. За яки й час долає цю ідстань другий велосипедист?
1298. Якщо одночасно відкрити дві труби різної пропускної здатності, то басейн буде наповнено водою за 6 год. Якщо відкрити обидві труби лише на 2 год, а потім залишити відкритою тільки одну з них, то решта басейну наповниться за 10 год. За скільки годин можна наповнити басейн через кожну трубу?
1299. Через першу трубу басейн можна наповнити водою за 12 год, а через Другу — за 24 год. Після кількох годин наповнення басейну через обидві труби першу трубу закрили. Решту об'єму басейну наповнювали 9 год через другу трубу. Скільки всього годин була відкрита друга труба?
1300. Довжина деталі на кресленні, виконаному в масштабі 1 : 30, дорівнює 2,5 см. Якою буде довжина цієї деталі на кресленні, масштаб якого 1 : 50?
1301. Щоб виміряти відстань між будинками А і В (рис. 166), орієнтувалися на дерево С, відстань від якого до будинку В дорівнює 300 м. За допомогою теодоліта виміряли кути ABC і АСВ, що дорівнюють відповідно 60° і 75°. Побудуйте зображення трикутника ABC у масштабі 1 : 6000. Виміряйте довжину зображення відрізка АВ та обчисліть відстань між будинками А і В.
1302. Запишіть у вигляді звичайного дробу:
1303. Зменшуване на 20 % більше за від'ємник. Скільки відсотків зменшуваного становить різниця?
1304. Кавові зерна в процесі підсмажування втрачають 12 % своєї маси. Скільки кілограмів свіжих зерен треба взяти, щоб отримати 6,6 кг смажених?
1305. Під час сушіння хліба на сухарі його маса зменшується на 35 %. Скільки кілограмів сухарів можна отримати зі 120 кг свіжого хліба?
1306. Містер Скрудж вклав у розвиток економіки Тридесятого царства 640 млн доларів, а через рік отримав 928 млн доларів прибутку. Скільки відсотків становив прибуток містера Скруджа? 640 млн доларів — 100%, 928 млн доларів — х%.
1307. Яке із двох чисел більше, якщо:
1308. Зібрали 15 кг білих грибів. У відходи пішло ЗО % маси грибів при підготовці їх до сушіння, а решта грибів втратила 76 % своєї маси під час сушіння. Скільки кілограмів сушених грибів отримали? 1) 100% - 30% = 70% — свіжих грибів для сушіння.
1309. На скільки відсотків збільшиться площа квадрата, якщо кожну його сторону збільшити на 10 %?
1310. Сторони прямокутника дорівнюють 20 см і 10 см. Одну сторону збільшили на 20 %, а сусідню зменшили на 20 %. Збільшилася чи зменшилася площа прямокутника та на скільки відсотків? Чи має значення, яку сторону збільшили, а яку — зменшили? Відповідь обґрунтуйте, розв'язавши задачу в загальному вигляді.
1311. Одна сторона прямокутника на 30 % більша за сторону квадрата, а сусідня на 30 % менша від сторони цього квадрата. Знайдіть відсоткове відношення площі прямокутника до площі квадрата.
1312. Периметр прямокутника дорівнює 76 см. Знайдіть площу прямокутника, якщо його сторони пропорційні числам 15 і 4.
1314. 1) Поділіть число 96 на три частини х, у і z так, щоб х : у = З : 4, а у : z = 4 : 9.
1314. 1) Поділіть число 96 на три частини x, y і z так, щоб x : y = 3 : 4, а y : z = 4 : 9. 2) Поділіть число 185 на три частини x, y і z так, щоб x : y = 3 : 2, а y : z = 2 1/2 : 3.
1315. Магазин продав за три дні партію яблук, причому першого дня було продано 9/20 маси яблук, а другого — 60 % решти. Скільки кілограмів яблук було продано за три дні, якщо за другий день продали 660 кг?
1316. Відстань між двома містами проїхали за 3 год. За першу годину проїхали 0, 3 усього шляху, за другу — 16/35 решти, а за третю — на 10, 5 км більше, ніж за другу. Знайдіть відстань між містами. 
1317. Накресліть: 1) гострокутний трикутник; 2) тупокутний трикутник; 3) прямокутний трикутник. Позначте всередині трикутника точку А та проведіть через неї прямі: а) перпендикулярні до сторін трикутника; б) паралельні сторонам трикутника.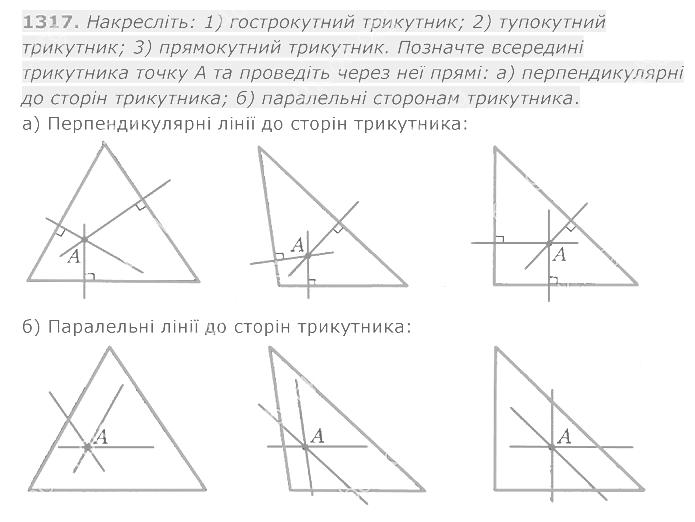
1318. Накресліть квадрат ABCD зі стороною 1 см і проведіть його діагоналі АС і BD. Через точки В і D проведіть прямі, перпендикулярні до прямої BD, а через А і С — прямі, паралельні прямій BD. Знайдіть точки перетину проведених прямих. Визначте вид многокутника, вершинами якого є ці точки, та знайдіть його площу.
1319. Перерисуйте в зошит рисунок 167, проведіть через точки В, М і К прямі, перпендикулярні до прямої AD.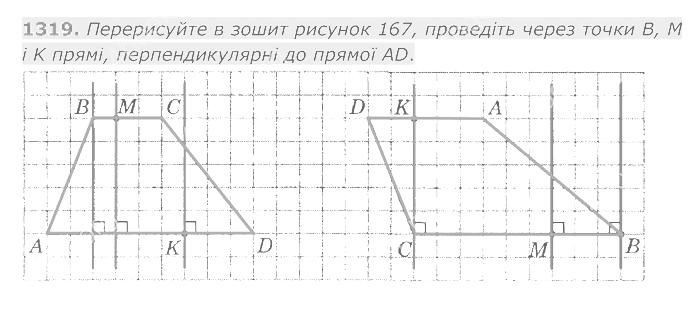
1320. Накресліть на координатній площині відрізки АВ і CD такі, що А (1; -2), В (4; 4), С (5; -1), D (-1; 1). Знайдіть координати точки перетину відрізків АВ і CD.
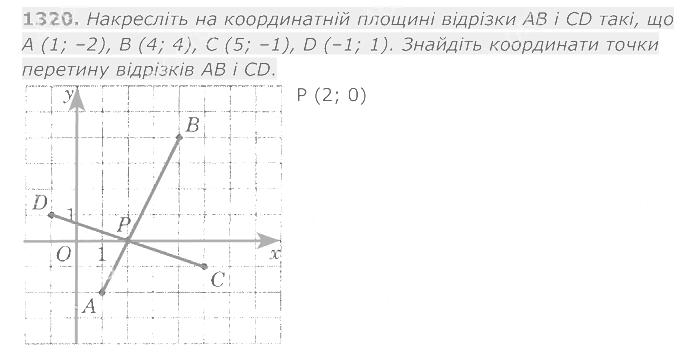1321. Побудуйте коло із центром у початку координат, що проходить через точку (-3; 4). Знайдіть координати точок перетину цього кола з осями координат та обчисліть довжину кола в одиничних відрізках координатних осей.
1322. На координатній площині позначте точки Е (-2; -6) і F (4; 3). Проведіть пряму EF і знайдіть: 1) координати точок перетину прямої EF з осями координат; 2) ординату точки, що належить прямій EF, ордината якої дорівнює 6.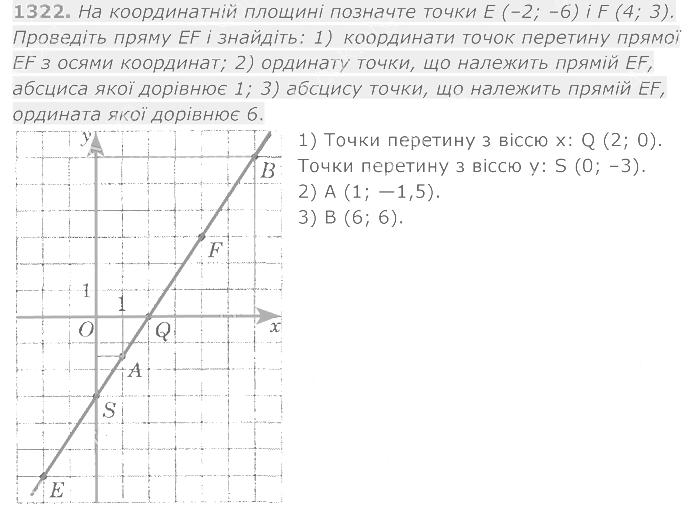
1323. Накресліть на координатній площині замкнену ламану, послідовними вершинами якої є точки з координатами: (-10; 6), (-9, 5 ; 8), (-8; 10), (-7; 10), (-6; 9), (-6; 7), (-7; 3), (-7; 1), (-6; 2), (-4; 3), (5; 3), (3; 1), (7; 3), (7; 2), (6; 1), (7; 1), (5; -1), (7; -1), (10; 0), (8; -3), (4; -4), (0; -4), (-4; -3), (-9; -4), (-10; -3), (-10; 0), (-7; 7), (-7; 8), ( -8; 7), (-9; 7). Позначте точку (-8, 5; 8, 5).
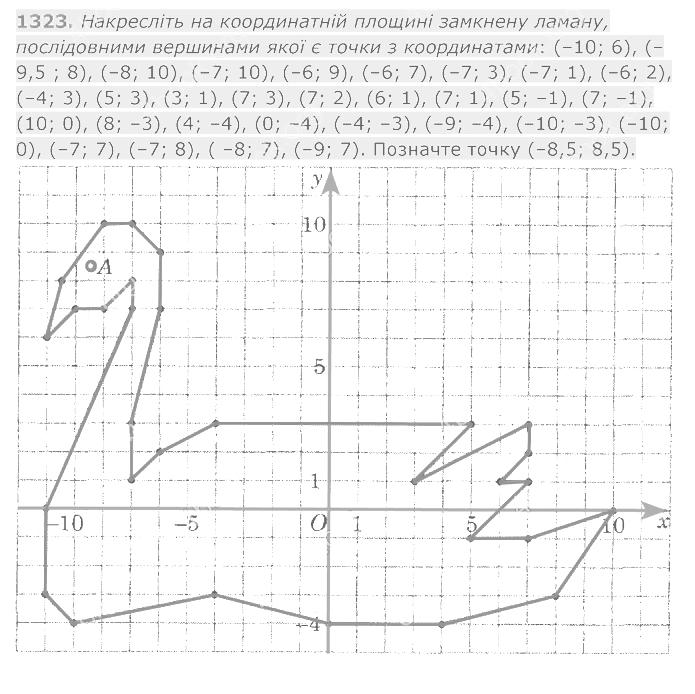1324. Накресліть на координатній площині замкнену ламану з вершинами в точках: (8; 9), (6; 8), (2; 8), (0; 9), (-4; 6), (-3; 2), (0; 0), (1; 2), (2; 1), (3; 1), (5; -1), (4; -2), (2; -2), (2; -3), (5; -3), (6; -2), (6; 2), (7; 0), (10; 3), (10; 7) ; ламану з вершинами в точках: (-4; 6), (-8; 5), (-11; 3), (-12; 0), (-14; -2), (-11; -1), (-10; -4), (-11; -8), (-8; -8), (-8; -7), (-7; -7), (-8; -3), (-3; -3), (-3; -9), (0; -9), (0; -4), (1; -4), (1; -5), (0; -7), (2; -9), (4; -5), (4; -3).
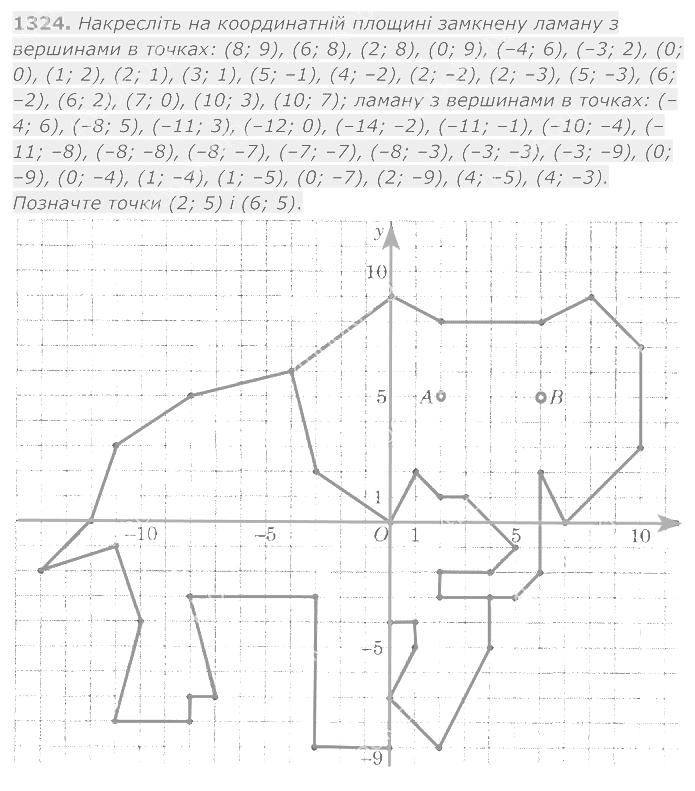1325. Одна зі сторін трикутника становить 0,6 другої, а третя сторона в 1,2 раза більша за другу. Знайдіть сторони трикутника, якщо його периметр дорівнює 21 дм.
1326. Розгорнутий кут поділили на три кути так, що градусна міра одного з утворених кутів становить 85 % градусної міри третього кута, а градусна міра другого — 40 % градусної міри третього.
1327. Прямий кут поділили на три кути так, що перший кут більший за другий на 14°, а третій менший від другого на 20°. Обчисліть градусні міри цих кутів і зробіть рисунок.
1328. У Сонячному місті протягом року похмурих днів було на 23 дні більше, ніж днів з дощем або снігом, і на 262 дні менше, ніж сонячних. Скільки було сонячних днів протягом цього року, якщо відомо, що він не був високосним?
1329. У шестикутнику п'ять сторін мають рівні довжини, а шоста відрізняється від них на 1, 2 см. Знайдіть сторони шестикутника, якщо його периметр дорівнює 37, 2 см. Скільки розв'язків має задача?1330. Довжина прямокутника становить 130 % ширини. Обчисліть площу прямокутника, якщо його периметр дорівнює 36, 8 см.
1330. Довжина прямокутника становить 130% ширини. Обчисліть площу прямокутника, якщо його периметр дорівнює 36,8 см.
1331. Земельні угіддя агрофірми мають площу 1220 га. Площа поля на 25 % більша за площу саду, а площа лугу на 80 га менша від площі саду. Знайдіть, яку площу окремо займають поле, сад і луг. Нехай площа саду становить х га. Тоді площа поля дорівнює 1, 25х га, а площа лугу — (х - 80) га. Відповідно до умови задачі складаємо рівняння;
1332. За два дні посадили 56 кущів троянд, причому другого дня посадили в 1 2/3 раза більше, ніж першого. Знайдіть, скільки кущів посадили першого дня і скільки — другого.
1333. За три дні продали 130 кг апельсинів. Другого дня продали 4/9 того, що продали першого, а третього — стільки, скільки за перші два дні разом. Скільки кілограмів апельсинів продали першого дня?
1334. Туристка подолала маршрут завдовжки 110 км за три дні. Другого дня вона пройшла на 5 км менше, ніж першого, а третього дня — 3/7 відстані, пройденої за перші два дні. Знайдіть, скільки кілометрів проходила туристка щодня.
1335. Із двох станцій, відстань між яким и дорівнює 360 км, одночасно вирушили назустріч один одному два поїзди. Швидкість одного з них на 10 км/год менша від швидкості другого. Знайдіть швидкість кожного поїзда, якщо вони зустрілися через 2,4 год після початку руху.
1336. Два автомобілі їдуть назустріч один одному. Швидкість першого дорівнює 75 км/год, що становить 5/6 швидкості другого. Другий автомобіль виїхав на 1, 6 год пізніше, ніж перший. Через скільки годин після виїзду другого автомобіля вони зустрінуться, якщо початкова відстань між ними становила 615 км?
1337. Вантажівка проїхала ґрунтовою дорогою на 210 км більше, ніж асфальтованою, причому довжина асфальтованої дороги становила 2/9 довжини ґрунтової. Час руху вантажівки асфальтованою дорогою становив 20 % часу руху ґрунтовою. Знайдіть швидкість руху вантажівки кожною з доріг, якщо всього вона була в дорозі 7, 2 год.
1338. Від села до станції Оксана може доїхати на велосипеді за З год, а дійти пішки — за 7 год. Її швидкість пішки на 8 км/год менша, ніж швидкість на велосипеді. З якою швидкістю їздить Оксана на велосипеді? Яка відстань від села до станції'?
1339. З одного міста в протилежних напрямках вирушили два пішоходи. Перший пішохід вийшов на 2, 5 год раніше від другого та йшов зі швидкістю 8 км/год. Швидкість другого становила 75 % швидкості першого. Через скільки годин після початку руху другого пішохода відстань між ними стала 41 км?
1340. З міста виїхав автомобіль зі швидкістю 48 км/год. Через півтори години в тому самому напрямку виїхав другий автомобіль, швидкість якого в 13/8 раза більша за швидкість першого. На якій відстані від міста другий автомобіль наздожене перший?
1341. Швидкість легкового автомобіля на 34 км/год більша за швидкість вантажного, тому вже за 3 год легковий автомобіль проїхав на 10 км більше, ніж вантажний за 5 год. Знайдіть швидкість кожного автомобіля.
1342. З пункту А до пункту В, відстань між якими 26 км, вийшов пішохід зі швидкістю 4 км/год. Через 12 хв з пункту В до пункту А назустріч йому виїхав велосипедист зі швидкістю 10 км/год. Через скільки годин після виїзду велосипедиста вони зустрілися? Яку відстань до зустрічі подолав кожен з них?
1343. Теплохід проходить відстань між двома пристанями й повертається назад (без зупинки) за 4, 5 год. Швидкість теплохода в стоячій воді становить 18 км/год, а швидкість течії річки — 2 км/год. Знайдіть відстань між пристанями.
1344. У три магазини завезли 680 кг апельсинів. Маса апельсинів, завезених у перший магазин, відноситься до маси апельсинів, завезених у другий, як 3 : 5, а в третій завезли на 12 % більше, ніж у другий. Скільки кілограмів апельсинів завезли в кожний магазин?
1345. Марічка та Софійка мали розв'язати за літо однакову кількість задач. Проте 28 серпня виявилося, що вони разом розв'язали 285 задач, причому Марічка перевиконала завдання на 8 %, а Софійка ще не розв'язала 18 % задач. Скільки задач мала розв'язати кожна дівчинка?
1346. На змаганнях стрільців із лука кожний учасник робив 20 пострілів. За кожний влучний постріл нараховували 15 очок, а за кожний промах знімали 7 очок. Робіну Гуду в око потрапила порошинка, тому він набрав лише 234 очки. Скільки разів Робін Гуд влучив у ціль?
1347. Оля і Толя задумали одне й те саме число. Потім Оля помножила своє число на 4, а Толя до свого числа додав 4. Далі Оля до отриманого результату додала число 3, а Толя свій результат помножив на 3. Після цього вони знову отримали рівні числа. Яке число задумали діти?
1348. Булочка з повидлом коштує 2 грн 40 коп. і ще 1/3 її ціни. Скільки коштує булочка?
1349. Яке одне й те саме число треба додати до чисельника та знаменника дробу 18/23, щоб отримати 5/6?
1350. Марина задумала два числа, одне з яких на 28 більше за друге. Які числа задумала Марина, якщо 60 % меншого числа становлять 25 % більшого?
1351. Івасик-Телесик пас на лузі гусей і кіз, у яких разом було 45 голів і 130 ніг. Скільки гусей і скільки кіз пас Івасик-Телесик?
1352. Бригада кроликів виростила врожай капусти, але не змогла його поділити порівну. Якби кожен кролик узяв по б качанів капусти, то 5 качанів залишилося би зайвими. А по 7 качанів вони взяти не могли, бо для цього їм не вистачало 5 качанів. Скільки кроликів було в бригаді? Скільки качанів капусти вони виростили? Нехай у бригаді було х кроликів. Якби кожен кролик узяв по 6 качанів капусти, то було б (6х + 5) качанів. Якби кожен кролик узя по 7 качанів капусти, то було б (7х - 5) качанів. Складаємо рівняння:
1353. Пан Богдан поклав у банк 20 000 грн на два види вкладу, причому по одному виду вкладу йому нараховували 6 % річних, а по другому — 9 %. Через рік чоловік отримав 1440 грн прибутку.
1354. У першому бідоні було в 4 рази більше молока, ніж у другому. Коли з першого бідона перелили в другий 20 л молока, то виявилося, що кількість молока в другому бідоні становить — того, що залишилося в першому. Скільки літрів молока було в кожному бідоні спочатку?
1355. Фермер привіз на базар бідон молока й за першу годину продав — молока. Якби він продав ще 20 л, то було б продано — усього молока. Скільки літрів молока було в бідоні?
1356. На полиці стояли книжки. Спочатку взяли на 2 книжки менше від третини всіх книжок, а потім половину книжок, що залишилися. Після цього на полиці стало 9 книжок. Скільки книжок було на полиці спочатку?
1357. Дві велосипедистки вирушили одночасно з двох міст назустріч одна одній. Коли вони зустрілися, то виявилося, що перша проїхала 4/9 усього шляху і ще 12 км, а друга — половину того, що проїхала перша. Знайдіть відстань між містами.
1358. Дванадцять хлопчиків обмінялися своїми адресами. Скільки адрес було роздано?
1359. У шаховому турнірі брали участь 12 гравців. Турнір проходив за круговою системою, тобто кожний учасник турніру грав з іншими по одному разу. Скільки всього ш ахових партій було зіграно?
1360. Розгадайте кросворд: італі: 3. Степінь. 4. Корінь. 5. Модуль. 8. Пропорція. 11. Перпендикулярні. 12. Мінус. 14. Центр. 16. Два. 17. Кратне. 18. Площа. По вертикалі: 1. Діаметр. 2. Ділення. 4. Коло. 6. Координатна. 7. Паралельні. 9. Ордината. 10. Куб. 13. Сектор. 15. Різниця. 16. Доданок. По горизонталі: 3. Добуток кількох рівних множників. 4. Розв'язок рівняння. 5. Відстань від точки координатної прямої до початку відліку. 8. Рівність двох відношень. 11. Прямі, при перетині яких утворюються прямі кути. 12. Символ, яким позначають від'ємні числа. 14. Точка, рівновіддалена від усіх точок кола. 16. Найменше просте число. 17. Число, яке ділиться націло на дане. 18. Величина. По вертикалі: і. Відрізок, що сполучає дві точки кола та проходить через його центр. 2. Математична дія. 4. Геометрична фігура. 6. Пряма, на якій позначено початок відліку, одиничний відрізок і напрямок. 7. Прямі, які лежать в одній площині і не мають спільних точок. 9. Одна з координат точки на площині. 10. Третій степінь числа. 13. Частина круга. 15. Результат дії віднімання. 16. Компонент дії додавання.
Назад
ГДЗ Підручник Математика Частина 2 2023 Мерзляк Полонський Якір Гімназія НУШ 6 клас
Якщо помітили в тексті помилку, виділіть її та натисніть Ctrl + Enter
![ГДЗ Природознавство 5 клас. Підручник [Ярошенко О.Г., Бойко В.М.] 2018](/uploads/posts/2019-04/1555779316_5_p_y_u2018.jpg "ГДЗ Природознавство 5 клас. Підручник [Ярошенко О.Г., Бойко В.М.] 2018")
![ГДЗ Основи правознавства 9 клас. Підручник [Наровлянський О. Д.] 2017](/uploads/posts/2019-02/1550928122_9k_p_n_2017.jpg "ГДЗ Основи правознавства 9 клас. Підручник [Наровлянський О. Д.] 2017")
![ГДЗ Українська мова 8 клас. Підручник [Глазова О.П.] 2021](/uploads/posts/2021-10/1633720388_8k_y_g_2021.jpg "ГДЗ Українська мова 8 клас. Підручник [Глазова О.П.] 2021")
![ГДЗ Вступ до історії 5 клас. Підручник [Гісем О.В.] 2018](/uploads/posts/2019-07/1564163269_5k_i_h_2018.jpg "ГДЗ Вступ до історії 5 клас. Підручник [Гісем О.В.] 2018")