ГДЗ Геометрія 8 клас. Підручник [Істер О.С.] 2021
§ 11. Середня лінія трапеції, її властивості
325. Основи трапеції дорівнюють 8 см і 4 см. Знайдіть середню лінію трапеції. 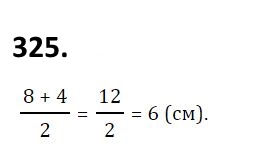 326. Знайдіть середню лінію трапеції, якщо її основи дорівнюють 7 см і 11 см.
326. Знайдіть середню лінію трапеції, якщо її основи дорівнюють 7 см і 11 см. 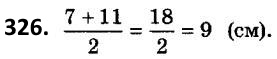 327. Знайдіть основу трапеції, якщо її друга основа дорівнює 9 см, а середня лінія - 7 см.
327. Знайдіть основу трапеції, якщо її друга основа дорівнює 9 см, а середня лінія - 7 см. 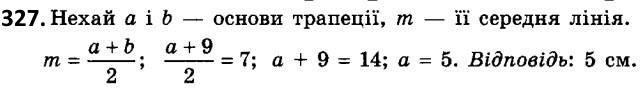 328. Одна з основ трапеції дорівнює 5 см, а середня лінія - 10 см. Знайдіть другу основу трапеції.
328. Одна з основ трапеції дорівнює 5 см, а середня лінія - 10 см. Знайдіть другу основу трапеції. 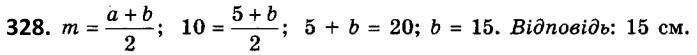 329. Одна з основ трапеції дорівнює 8 см, а друга - удвічі більша за неї. Знайдіть відстань між серединами бічних сторін трапеції.
329. Одна з основ трапеції дорівнює 8 см, а друга - удвічі більша за неї. Знайдіть відстань між серединами бічних сторін трапеції. 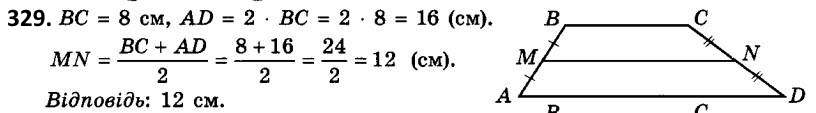 330. Середня лінія трапеції дорівнює 30 см. Знайдіть основи трапеції, якщо: 1) одна з них на 8 см більша за другу; 2) одна з них у 4 рази менша від другої; 3) вони відносяться як 3 : 2.
330. Середня лінія трапеції дорівнює 30 см. Знайдіть основи трапеції, якщо: 1) одна з них на 8 см більша за другу; 2) одна з них у 4 рази менша від другої; 3) вони відносяться як 3 : 2.  331. Середня лінія трапеції дорівнює 16 см. Знайдіть основи трапеції, якщо: 1) одна з них на 2 см менша від другої; 2) одна з них утричі більша за другу; 3) їх відношення дорівнює 3 : 5.
331. Середня лінія трапеції дорівнює 16 см. Знайдіть основи трапеції, якщо: 1) одна з них на 2 см менша від другої; 2) одна з них утричі більша за другу; 3) їх відношення дорівнює 3 : 5.  333. Бічні сторони трапеції дорівнюють 7 см і 9 см, а її середня лінія - 10 см. Знайдіть периметр трапеції.
333. Бічні сторони трапеції дорівнюють 7 см і 9 см, а її середня лінія - 10 см. Знайдіть периметр трапеції. 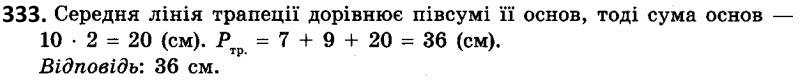 334. Бічні сторони трапеції дорівнюють 10 см і 12 см, а її периметр - 52 см. Знайдіть середню лінію трапеції.
334. Бічні сторони трапеції дорівнюють 10 см і 12 см, а її периметр - 52 см. Знайдіть середню лінію трапеції.  335. Чи може середня лінія трапеції: 1) дорівнювати одній з основ; 2) бути меншою від меншої основи; 3) бути більшою за більшу основу; 4) бути вдвічі меншою від більшої основи?
335. Чи може середня лінія трапеції: 1) дорівнювати одній з основ; 2) бути меншою від меншої основи; 3) бути більшою за більшу основу; 4) бути вдвічі меншою від більшої основи?  336. EF - середня лінія трапеції ABCD, яка перетинає діагональ BD у точці N. EN = 5 см, NF = 3 см. Знайдіть основи трапеції.
336. EF - середня лінія трапеції ABCD, яка перетинає діагональ BD у точці N. EN = 5 см, NF = 3 см. Знайдіть основи трапеції.  337. MN - середня лінія трапеції ABCD, яка перетинає діагональ AC у точці K. Знайдіть MK і KN, якщо основи трапеції дорівнюють 18 см і 12 см.
337. MN - середня лінія трапеції ABCD, яка перетинає діагональ AC у точці K. Знайдіть MK і KN, якщо основи трапеції дорівнюють 18 см і 12 см.  338. У трапеції ABCD AD = 30 см, BC = 12 см - основи, а точки E і T - середини AB і AE відповідно. Через E і T проведено прямі, паралельні AD. Знайдіть відрізки цих прямих, що містяться між бічними сторонами трапеції.
338. У трапеції ABCD AD = 30 см, BC = 12 см - основи, а точки E і T - середини AB і AE відповідно. Через E і T проведено прямі, паралельні AD. Знайдіть відрізки цих прямих, що містяться між бічними сторонами трапеції. 339. У трапеції ABCD M - середина бічної сторони AB, N - середина MB. Через точки M і N проведено прямі, паралельні BC, які перетинають CD у точках K і L відповідно. MK = 12 см, NL = 8 см. Знайдіть основи трапеції.
339. У трапеції ABCD M - середина бічної сторони AB, N - середина MB. Через точки M і N проведено прямі, паралельні BC, які перетинають CD у точках K і L відповідно. MK = 12 см, NL = 8 см. Знайдіть основи трапеції. 340. У рівнобічній трапеції ABCD перпендикуляр, проведений з вершини B на більшу основу AD трапеції, ділить її на відрізки 3 см і 7 см. Знайдіть середню лінію трапеції.
340. У рівнобічній трапеції ABCD перпендикуляр, проведений з вершини B на більшу основу AD трапеції, ділить її на відрізки 3 см і 7 см. Знайдіть середню лінію трапеції.  341. З вершини B тупого кута рівнобічної трапеції ABCD проведено висоту BK до основи AD. AK = 4 см, BC = 6 см. Знайдіть середню лінію трапеції.
341. З вершини B тупого кута рівнобічної трапеції ABCD проведено висоту BK до основи AD. AK = 4 см, BC = 6 см. Знайдіть середню лінію трапеції.  342. Точки A і B лежать по один бік від прямої l. Відстань до неї від точки A дорівнює 7 см, а від точки M, яка є серединою AB, - 5 см. Знайдіть відстань від точки B до прямої l.
342. Точки A і B лежать по один бік від прямої l. Відстань до неї від точки A дорівнює 7 см, а від точки M, яка є серединою AB, - 5 см. Знайдіть відстань від точки B до прямої l. 343. По один бік від прямої а на відстані 10 см і 16 см від неї позначено точки M і N. Знайдіть відстань від середини відрізка MN до прямої а.
343. По один бік від прямої а на відстані 10 см і 16 см від неї позначено точки M і N. Знайдіть відстань від середини відрізка MN до прямої а.  344. Основи трапеції дорівнюють 6 см і 14 см. Діагоналі трапеції ділять її середню лінію на три частини. Знайдіть довжини цих частин.
344. Основи трапеції дорівнюють 6 см і 14 см. Діагоналі трапеції ділять її середню лінію на три частини. Знайдіть довжини цих частин.  345. Діагоналі ділять середню лінію трапеції на три частини, довжини яких 7 см, 8 см і 7 см. Знайдіть основи трапеції.
345. Діагоналі ділять середню лінію трапеції на три частини, довжини яких 7 см, 8 см і 7 см. Знайдіть основи трапеції.  346. У трапеції ABCD (AD || BC) ZA = 90°, ZC = 135°, AB = 6 см. Знайдіть середню лінію трапеції, якщо її діагональ перпендикулярна до бічної сторони.
346. У трапеції ABCD (AD || BC) ZA = 90°, ZC = 135°, AB = 6 см. Знайдіть середню лінію трапеції, якщо її діагональ перпендикулярна до бічної сторони.  347. Діагональ рівнобічної трапеції ділить навпіл тупий кут трапеції, а її середню лінію - на відрізки 4 см і 6 см. Знайдіть периметр трапеції.
347. Діагональ рівнобічної трапеції ділить навпіл тупий кут трапеції, а її середню лінію - на відрізки 4 см і 6 см. Знайдіть периметр трапеції.  348. Діагональ рівнобічної трапеції ділить її гострий кут навпіл, а середню лінію - на відрізки 3 см і 7 см. Знайдіть периметр трапеції.
348. Діагональ рівнобічної трапеції ділить її гострий кут навпіл, а середню лінію - на відрізки 3 см і 7 см. Знайдіть периметр трапеції. 349. Знайдіть кути M і N чотирикутника MNKL, вписаного в коло, якщо ZK = 37°, ZL = 119°.
349. Знайдіть кути M і N чотирикутника MNKL, вписаного в коло, якщо ZK = 37°, ZL = 119°.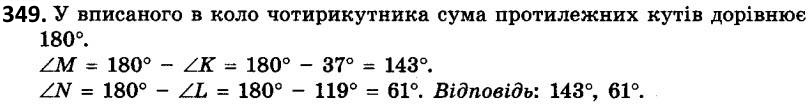 350. Коло вписано в рівнобічну трапецію, бічна сторона якої дорівнює а см. Знайдіть периметр трапеції.
350. Коло вписано в рівнобічну трапецію, бічна сторона якої дорівнює а см. Знайдіть периметр трапеції. 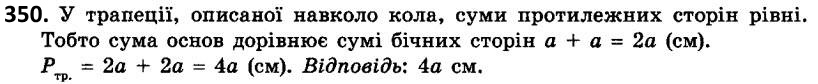 351. У прямокутній трапеції тупий кут дорівнює 120°, більша основа - 14 см, а більша бічна сторона - 8 см. Знайдіть меншу основу трапеції.
351. У прямокутній трапеції тупий кут дорівнює 120°, більша основа - 14 см, а більша бічна сторона - 8 см. Знайдіть меншу основу трапеції. 353. Усі стінки й дно картонної коробки без кришки мають форму квадрата зі стороною a. Розріжте розгортку коробки двома розрізами так, щоб з отриманих частин можна було скласти квадрат, площа якого дорівнює 5а^2.
353. Усі стінки й дно картонної коробки без кришки мають форму квадрата зі стороною a. Розріжте розгортку коробки двома розрізами так, щоб з отриманих частин можна було скласти квадрат, площа якого дорівнює 5а^2.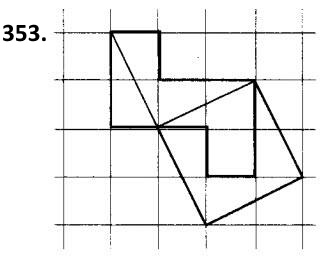
 ГДЗ 2021 Геометрія Істер Підручник 8 клас Генеза
ГДЗ 2021 Геометрія Істер Підручник 8 клас Генеза
 Якщо помітили в тексті помилку, виділіть її та натисніть Ctrl + Enter
Якщо помітили в тексті помилку, виділіть її та натисніть Ctrl + Enter 22.10.2021,
22.10.2021,
 39 415,
39 415,
 0
0
 Назад
Назад




![ГДЗ Природознавство 5 клас. Підручник [Ярошенко О.Г., Бойко В.М.] 2018 ГДЗ Природознавство 5 клас. Підручник [Ярошенко О.Г., Бойко В.М.] 2018](/uploads/posts/2019-04/1555779316_5_p_y_u2018.jpg)
![ГДЗ Основи правознавства 9 клас. Підручник [Наровлянський О. Д.] 2017 ГДЗ Основи правознавства 9 клас. Підручник [Наровлянський О. Д.] 2017](/uploads/posts/2019-02/1550928122_9k_p_n_2017.jpg)
![ГДЗ Українська мова 8 клас. Підручник [Глазова О.П.] 2021 ГДЗ Українська мова 8 клас. Підручник [Глазова О.П.] 2021](/uploads/posts/2021-10/1633720388_8k_y_g_2021.jpg)
![ГДЗ Вступ до історії 5 клас. Підручник [Гісем О.В.] 2018 ГДЗ Вступ до історії 5 клас. Підручник [Гісем О.В.] 2018](/uploads/posts/2019-07/1564163269_5k_i_h_2018.jpg)