ГДЗ Геометрія 8 клас. Підручник [Істер О.С.] 2021

648. (Усно) (MKL - прямокутний, ZM = 90° (мал. 180). Які з рівностей правильні: 1) KM2 = ML2 - KL2; 2) KL2 = ML2 + KM2; 3) ML2 = KL2 + KM2; 4) KM2 = KL2 - ML2; 5) KL2 = ML2 - KM2; 6) ML2 = KL2 - KM2?
649. EFP - прямокутанй, ZP = 90°. Заповніть пропуски: 1) EF2 = ...2+ ...2; 2) EP2 = ...2 - ...2.
650. Знайдіть гіпотенузу прямокутного трикутника, якщо його катети дорівнюють: 1) 6 см і 8 см; 2) 12 см і 35 см.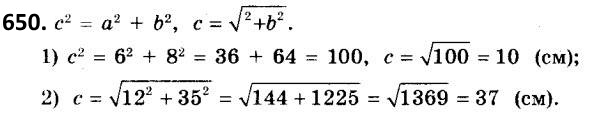
651. Знайдіть гіпотенузу прямокутного трикутника, якщо його катети дорівнюють: 1) 5 см і 12 см; 2) 8 см і 15 см. 
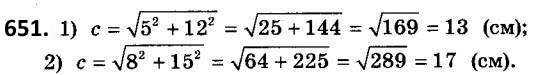652. Знайдіть невідомий катет прямокутного трикутника, якщо його гіпотенуза та другий катет відповідно дорівнюють: 1) 17 см і 8 см; 2) 26 см і 10 см. 
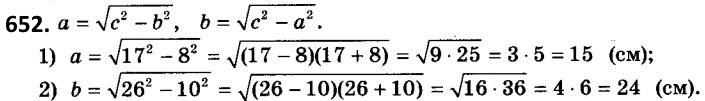653. Знайдіть невідомий катет прямокутного трикутника, якщо його гіпотенуза та другий катет відповідно дорівнюють: 1) 25 см і 7 см; 2) 41 см і 40 см. 
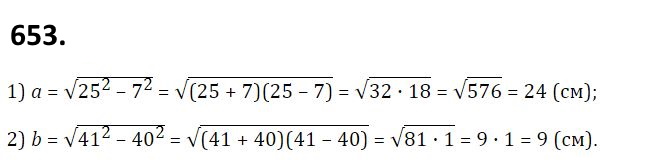656. Дві більші сторони прямокутного трикутника дорівнюють 7 см і 5 см. Знайдіть його найменшу сторону.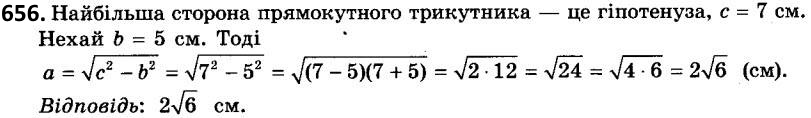 

657. Дві менші сторони прямокутного трикутника дорівнюють 2 см і 3 см. Знайдіть його найбільшу сторону. 
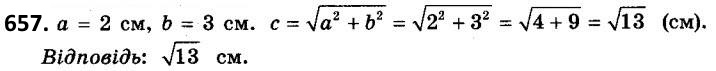658. Сторони прямокутника дорівнюють 6 см і 8 см. Знайдіть його діагональ.
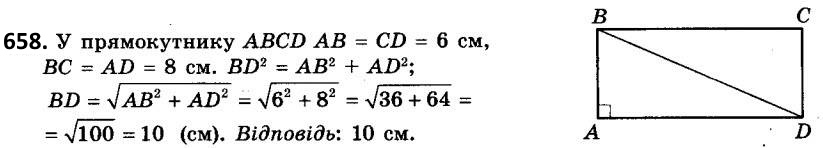659. Діагональ прямокутника дорівнює 13 см, а одна з його сторін - 12 см. Знайдіть другу сторону прямокутника. 
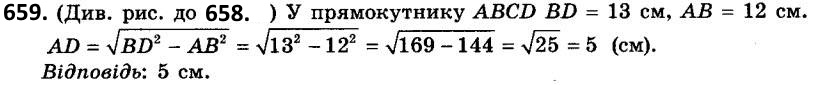660. Бічна сторона рівнобедреного трикутника дорівнює 15 см, а висота, проведена до основи, - 12 см. Знайдіть основу трикутника. 
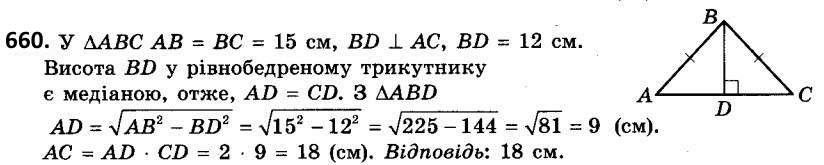661. Основа рівнобедреного трикутника дорівнює 16 см, а висота, проведена до основи, - 15 см. Знайдіть бічну сторону трикутника. 
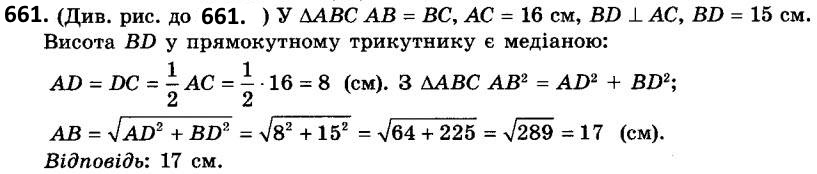662. Діагоналі ромба дорівнюють 24 см і 70 см. Знайдіть сторону ромба. 
663. Сторона ромба дорівнює 13 см, а одна з діагоналей - 10 см. Знайдіть другу діагональ ромба.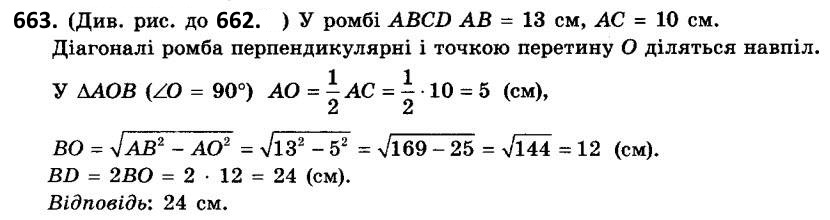 
664. Діагональ квадрата дорівнює 3\/2 см. Знайдіть його сторону. 
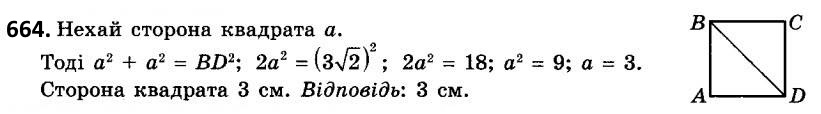665. Катети прямокутного трикутника дорівнюють 7 см і 8 см. Знайдіть довжину медіани, проведеної до більшого катета. 
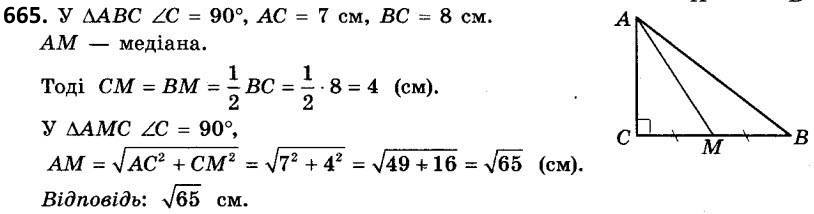666. Катети прямокутного трикутника дорівнюють 6 см і 9 см. Знайдіть довжину медіани, проведеної до меншого катета. 
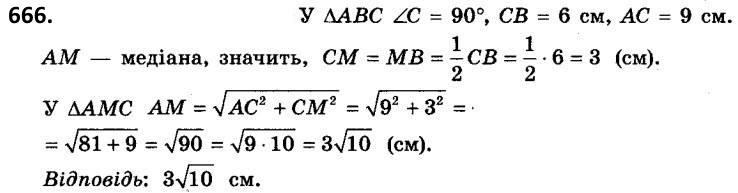667. З точки A до кола із центром O проведено дотичну, B - точка дотику. Знайдіть довжину відрізка AO, якщо OB = 2 см, AB = 7 см.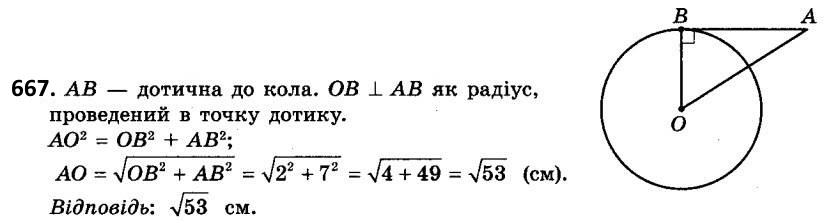 

668. З точки M до кола із центром O проведено дотичну, P - точка дотику. Знайдіть довжину відрізка PM, якщо OP = 3 см, OM = 6 см. 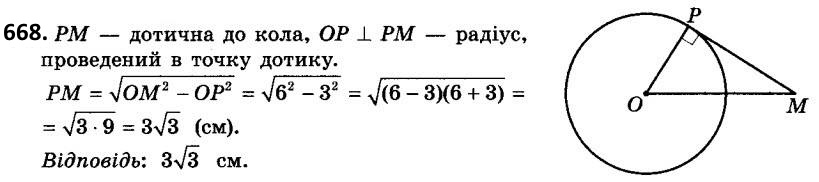669. Чи є прямокутним трикутник зі сторонами: 1) 15; 20; 25; 2) 4; 5; 6? 
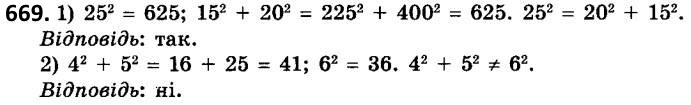670. Чи є прямокутним трикутник зі сторонами: 1) 5; 6; 9; 2) 16; 30; 34? 
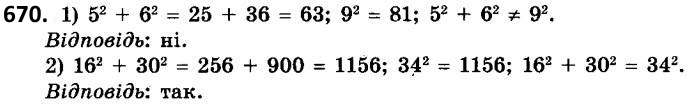671. У колі, радіус якого дорівнює 13 см, проведено хорду, завдовжки 10 см. Знайдіть відстань від центра кола до даної хорди. 
672. У колі проведено хорду завдовжки 16 см. Знайдіть радіус кола, якщо відстань від центра кола до хорди дорівнює 6 см.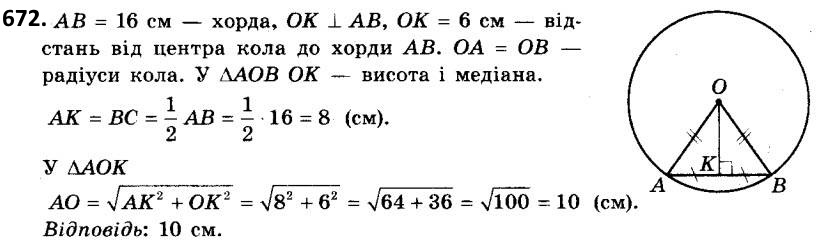
673. Дві сторони прямокутного трикутника дорівнюють 5 см і 6 см. Знайдіть третю сторону (розгляньте всі випадки). 
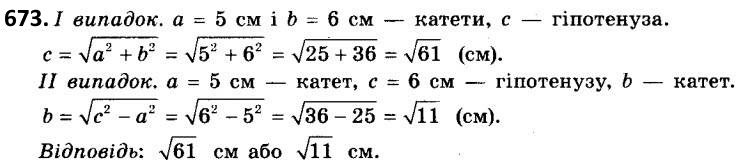674. Дві сторони прямокутного трикутника дорівнюють 5 см і 2 см. Знайдіть третю сторону (розгляньте всі випадки). 
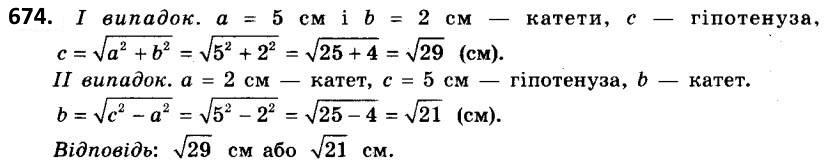677. Катети прямокутного трикутника відносяться як 7 : 24, а гіпотенуза дорівнює 50 см. Знайдіть периметр трикутника. 
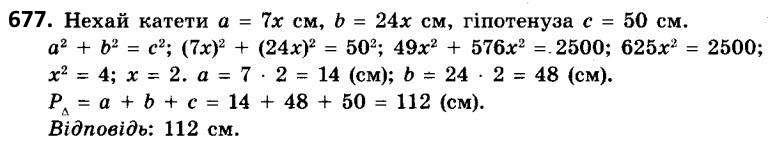678. Катет відноситься до гіпотенузи як 8 : 17. Знайдіть периметр трикутника, якщо другий катет дорівнює 30 см. 
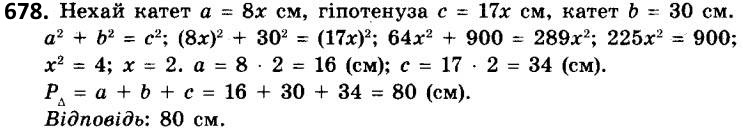679. Знайдіть довжину невідомого відрізка x на малюнках 185-188.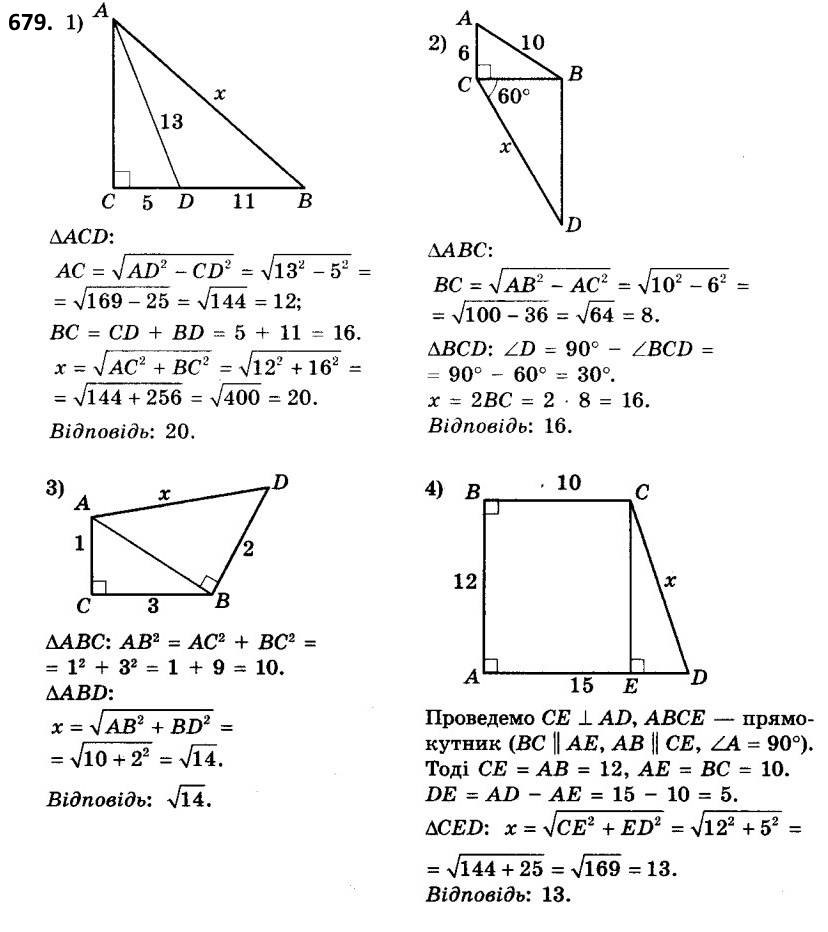

680. Знайдіть довжину невідомого відрізка x на малюн ках 189 і 190.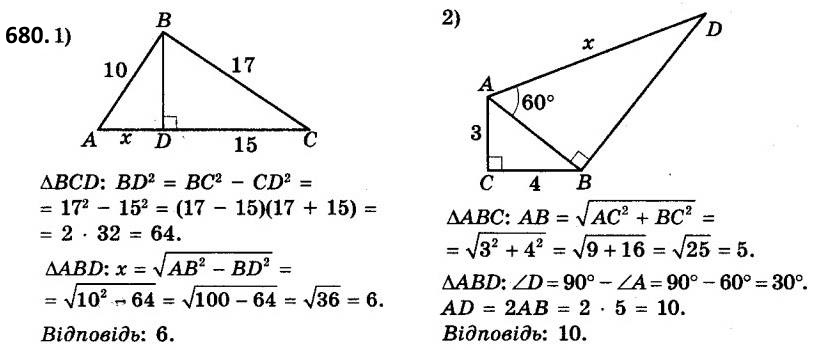681. Один з катетів прямокутного трикутника дорівнює 6 см, а другий на 2 см менший від гіпотенузи. Знайдіть периметр трикутника. 
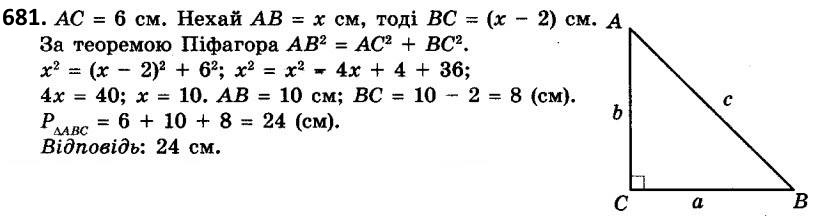682. Один з катетів прямокутного трикутника дорівнює 5 см, а гіпотенуза на 1 см більша за другий катет. Знайдіть периметр трикутника. 
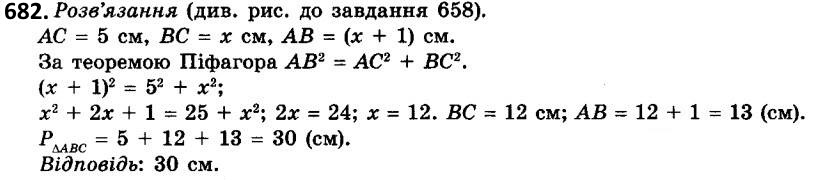683. У трикутникуABC кут A тупий, BC = 39 см, AB = 17 см. BK - висота трикутника, BK = 15 см. Знайдіть AC. 
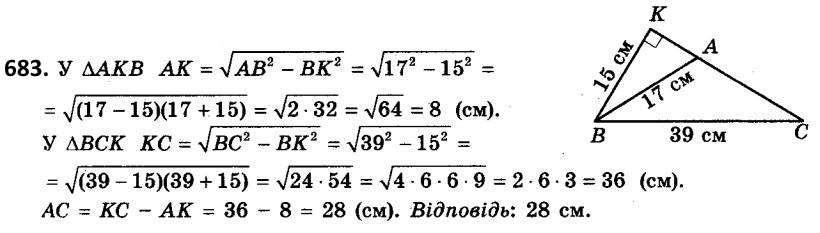684. BK - висота трикутника ABC, у якого ZC - тупий. AB = 20 см, BC = 13 см, CK = 5 см. Знайдіть AC. 
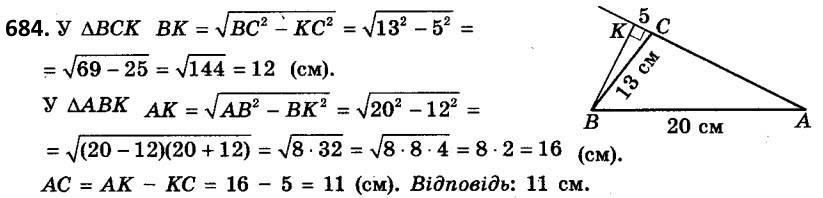685. У рівнобедреному трикутнику висота, проведена до бічної сторони, дорівнює 5 см і поділяє її на два відрізки так, що прилеглий до вершини рівнобедреного трикутника відрізок дорівнює 12 см. Знайдіть основу трикутника. 
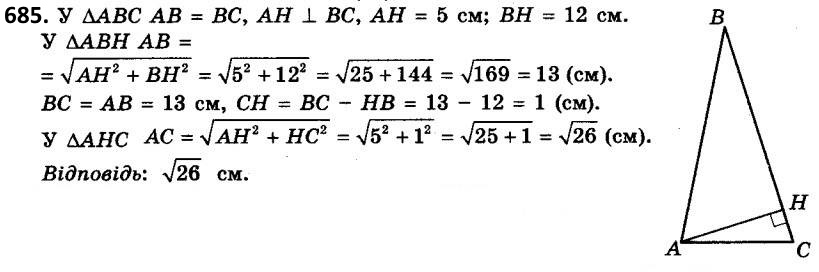686. Висота BK рівнобедреного трикутника ABC (AB = AC) ділить сторону AC на відрізки AK = 24 см і KC = 1 см. Знайдіть основу трикутника.
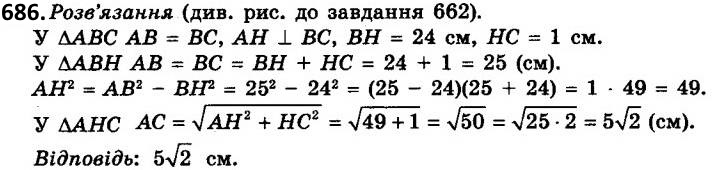687. Знайдіть сторони паралелограма, діагоналі якого дорівнюють 8 см і 10 см й одна з них перпендикулярна до сторони. 
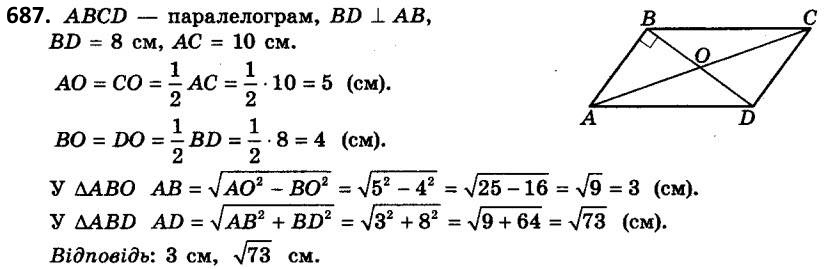688. Радіус кола, описаного навколо тупокутного рівнобедреного трикутника, дорівнює 37 см, а його основа - 70 см. Знайдіть бічну сторону трикутника. 
689. Висота рівнобедреного гострокутного трикутника, проведена до основи, дорівнює 18 см, а радіус кола, описаного навколо нього, - 13 см. Знайдіть бічну сторону трикутника. 
690. Побудуйте відрізок, довжина якого дорівнює. 
691. Побудуйте відрізок, довжина якого дорівнює. 
692. Бісектриса гострого кута прямокутного трикутника ділить катет на відрізки завдовжки 10 см і 26 см. Знайдіть периметр трикутника.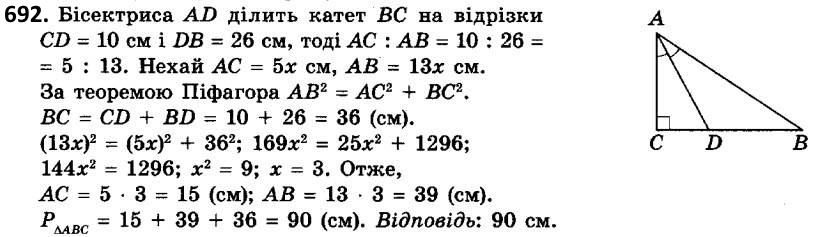 
693. Бісектриса прямого кута трикутника ділить гіпотенузу на відрізки, що дорівнюють 15 см і 20 см. Знайдіть периметр трикутника. 
694. У прямокутному трикутнику точка дотику вписаного кола ділить катет на відрізки 2 см і 10 см. Знайдіть периметр трикутника. 
695. Діагоналі трапеції взаємно перпендикулярні й дорівнюють 6 см і 8 см. Знайдіть середню лінію трапеції.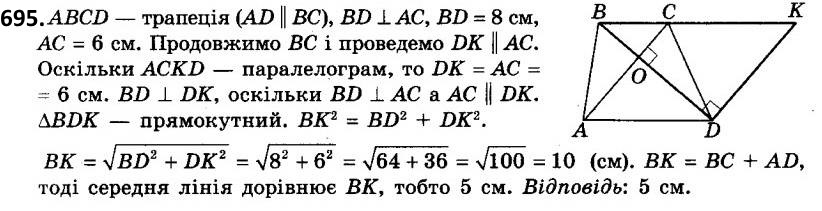
696. Рівнобічну трапецію з основами а і b описано навколо кола. Доведіть, що її висота дорівнює. 
697. Відношення бічної сторони до основи рівнобедреного трикутника дорівнює 5 : 8, а різниця відрізків, на які бісектриса кута при основі ділить висоту, проведену до основи, дорівнює 3 см. Знайдіть периметр трикутника. 
698. Бічна сторона рівнобедреного трикутника на 5 см менша від основи. Відрізки, на які бісектриса кута при основі ділить висоту, проведену до основи, відносяться як 5 : 3. Знайдіть периметр трикутника.
699. Один з кутів прямокутного трикутника дорівнює 30°. Знайдіть медіану цього трикутника, проведену до гіпотенузи, якщо сума гіпотенузи й меншого катета дорівнює 18 см.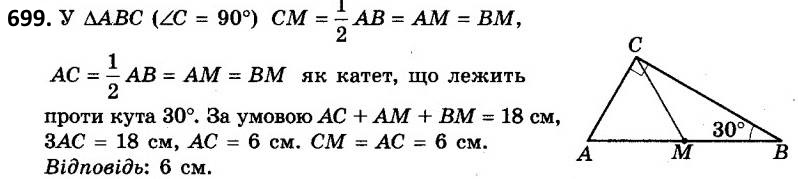 
700. Коло радіуса 3 см вписано в ромб. Один з відрізків, на які точка дотику ділить сторону ромба, дорівнює 9 см. Знайдіть периметр ромба.
701. Трапецію вписано в коло так, що діаметр кола є її більшою основою, а відношення основ дорівнює 2 : 1. Знайдіть кути трапеції.
702. Побудуйте пряму m та точку A на відстані 2 см від прямої m і точку B на відстані 3 см від прямої m. 
704. Побудуйте паралельні прямі, відстань між якими дорівнює 2 см.
706. Чи можна розмістити на площині 6 точок так, щоб будьякі три з них були вершинами рівнобедреного трикутника?

---

---

Назад

Вперед

1 ... 32 33 34 35 36 37 38 39 40 ... 67

ГДЗ 2021 Геометрія Істер Підручник 8 клас Генеза