ГДЗ Геометрія 8 клас. Підручник [Істер О.С.] 2021
Задачі підвищеної складності
Розділ 1. Чотирикутники
1044. На сторонах AB і CD паралелограма ABCD зовні нього побудовано два рівносторонніх трикутники ABK і CDL. Доведіть, що відрізок KL проходить через точку перетину діагоналей паралелограма. Розділ 1. Чотирикутники
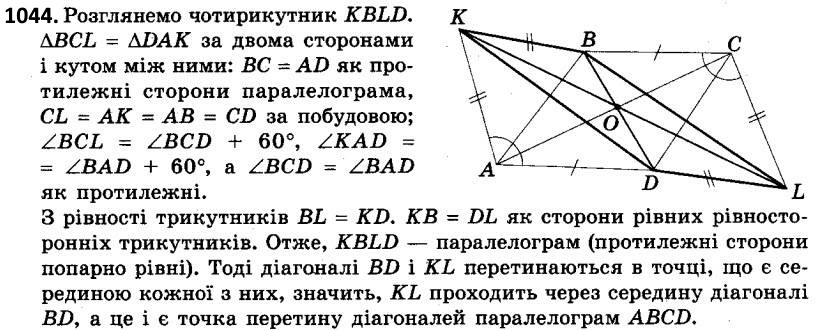 1045. На основі AB рівнобедреного трикутника ABC взято довільну точку K. Через цю точку паралельно BC і AC проведено прямі, які перетинають сторони трикутника. Доведіть, що периметр паралелограма, який при цьому утворився, не залежить від положення точки K.
1045. На основі AB рівнобедреного трикутника ABC взято довільну точку K. Через цю точку паралельно BC і AC проведено прямі, які перетинають сторони трикутника. Доведіть, що периметр паралелограма, який при цьому утворився, не залежить від положення точки K.  1046. Точки A, B і C лежать на колі із центром O. ABCO - паралелограм. Знайдіть його кути.
1046. Точки A, B і C лежать на колі із центром O. ABCO - паралелограм. Знайдіть його кути.  1047. Побудуйте паралелограм за двома діагоналями й висотою.
1047. Побудуйте паралелограм за двома діагоналями й висотою.  1048. Діагоналі опуклого чотирикутника розбивають його на чотири трикутники, периметри яких однакові. Визначте вид чотирикутника.
1048. Діагоналі опуклого чотирикутника розбивають його на чотири трикутники, периметри яких однакові. Визначте вид чотирикутника. 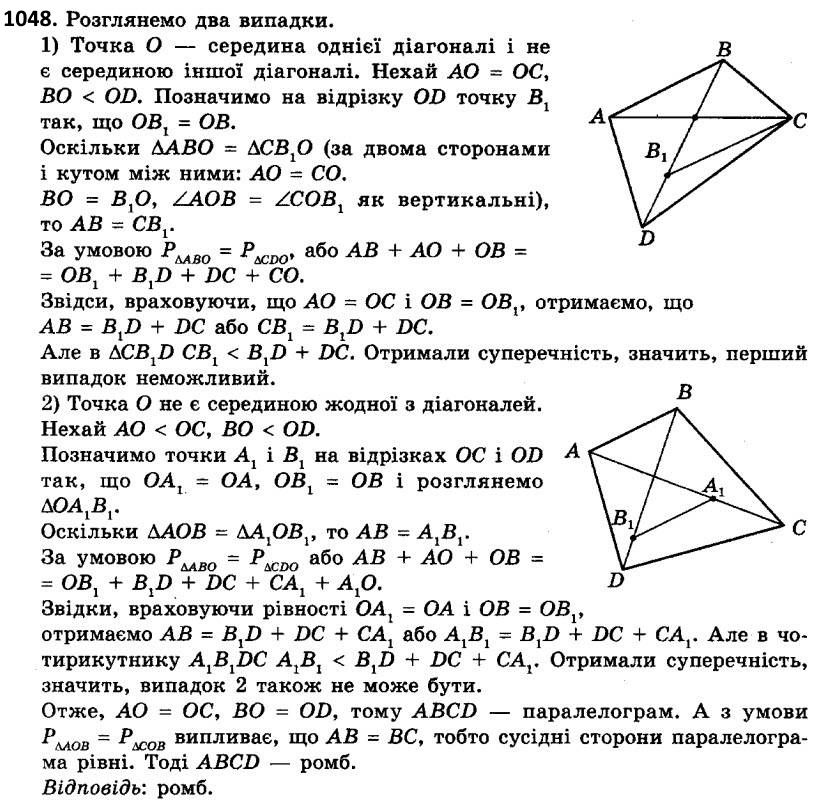 1049. Коло з діаметром AC проходить через середину сторони AB ромба ABCD. Знайдіть тупий кут ромба.
1049. Коло з діаметром AC проходить через середину сторони AB ромба ABCD. Знайдіть тупий кут ромба.  1050. Зовні прямокутника ABCD вибрано точку K так, що ZAKC = 90°. Знайдіть ZDKB.
1050. Зовні прямокутника ABCD вибрано точку K так, що ZAKC = 90°. Знайдіть ZDKB.  1051. На катетах AC і BC прямокутного трикутника ABC побудовано квадрати ACDE і BCKL. Прямі ED і KL перетинаються в точці P. Під яким кутом перетинаються прямі PC і AB?
1051. На катетах AC і BC прямокутного трикутника ABC побудовано квадрати ACDE і BCKL. Прямі ED і KL перетинаються в точці P. Під яким кутом перетинаються прямі PC і AB?  1052. Сторони прямокутника дорівнюють а і b (a > b). Бісектриси чотирьох кутів прямокутника, перетинаючись, утворюють чотирикутник. Знайдіть його діагоналі.
1052. Сторони прямокутника дорівнюють а і b (a > b). Бісектриси чотирьох кутів прямокутника, перетинаючись, утворюють чотирикутник. Знайдіть його діагоналі.  1053. Доведіть, що бісектриса кута паралелограма ділить навпіл кут між висотами, проведеними з вершини цього кута.
1053. Доведіть, що бісектриса кута паралелограма ділить навпіл кут між висотами, проведеними з вершини цього кута. 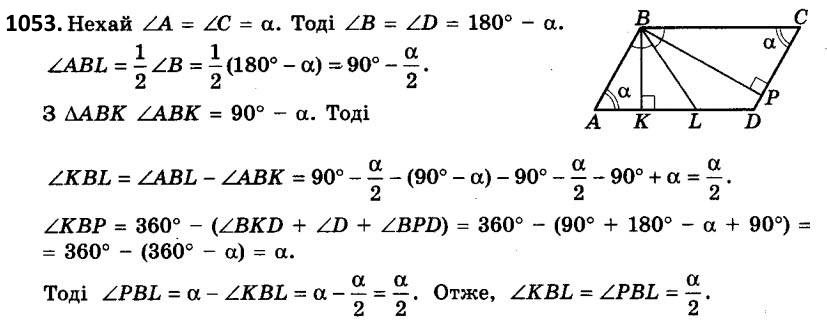 1054. Усередині квадрата ABCD узято точку P і на відрізку AP, як на стороні, побудовано квадрат APNM, сторона якого PN перетинає сторону AD квадрата ABCD. Порівняйте між собою відрізки BP і DM.
1054. Усередині квадрата ABCD узято точку P і на відрізку AP, як на стороні, побудовано квадрат APNM, сторона якого PN перетинає сторону AD квадрата ABCD. Порівняйте між собою відрізки BP і DM.  1055. Доведіть, що в будь-якій трапеції сума бічних сторін більша за різницю більшої і меншої основ.
1055. Доведіть, що в будь-якій трапеції сума бічних сторін більша за різницю більшої і меншої основ. 1056. Відомо, що існує точка, рівновіддалена від усіх прямих, що містять сторони трапеції. Знайдіть периметр трапеції, якщо її середня лінія дорівнює 10 см.
1056. Відомо, що існує точка, рівновіддалена від усіх прямих, що містять сторони трапеції. Знайдіть периметр трапеції, якщо її середня лінія дорівнює 10 см.  1057. Відомо, що існує точка, рівновіддалена від усіх вершин трапеції, один з кутів якої дорівнює 40°. Знайдіть інші кути трапеції.
1057. Відомо, що існує точка, рівновіддалена від усіх вершин трапеції, один з кутів якої дорівнює 40°. Знайдіть інші кути трапеції.  1058. Основи трапеції дорівнюють а і b (a > b), а сума кутів, прилеглих до більшої основи, дорівнює 90°. Знайдіть відстань між серединами основ трапеції.
1058. Основи трапеції дорівнюють а і b (a > b), а сума кутів, прилеглих до більшої основи, дорівнює 90°. Знайдіть відстань між серединами основ трапеції. 1059. Діагоналі чотирикутника ABCD, вписаного в коло, перетинаються в точці M. Відомо, що ZABC = 73°, ZBCD = 103°, ZAMD = 110°. Знайдіть ZACD.
1059. Діагоналі чотирикутника ABCD, вписаного в коло, перетинаються в точці M. Відомо, що ZABC = 73°, ZBCD = 103°, ZAMD = 110°. Знайдіть ZACD.  1060. У гострокутному трикутнику ABC проведено висоти AH1, BH2 і CH3. H - точка їхнього перетину. Серед семи точок A, B, C, H1, H2, H3 і H укажіть усі такі їхні четвірки, через які можна провести коло.
1060. У гострокутному трикутнику ABC проведено висоти AH1, BH2 і CH3. H - точка їхнього перетину. Серед семи точок A, B, C, H1, H2, H3 і H укажіть усі такі їхні четвірки, через які можна провести коло.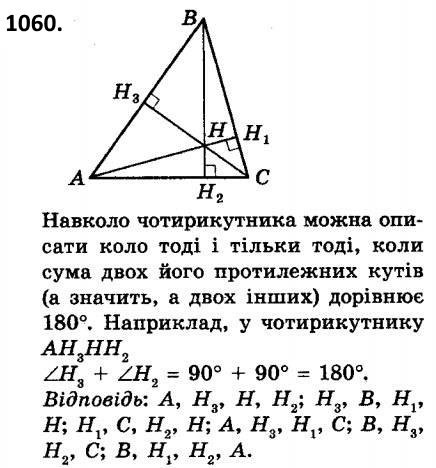
 ГДЗ 2021 Геометрія Істер Підручник 8 клас Генеза
ГДЗ 2021 Геометрія Істер Підручник 8 клас Генеза
 Якщо помітили в тексті помилку, виділіть її та натисніть Ctrl + Enter
Якщо помітили в тексті помилку, виділіть її та натисніть Ctrl + Enter 22.10.2021,
22.10.2021,
 39 415,
39 415,
 0
0
 Назад
Назад




![ГДЗ Природознавство 5 клас. Підручник [Ярошенко О.Г., Бойко В.М.] 2018 ГДЗ Природознавство 5 клас. Підручник [Ярошенко О.Г., Бойко В.М.] 2018](/uploads/posts/2019-04/1555779316_5_p_y_u2018.jpg)
![ГДЗ Основи правознавства 9 клас. Підручник [Наровлянський О. Д.] 2017 ГДЗ Основи правознавства 9 клас. Підручник [Наровлянський О. Д.] 2017](/uploads/posts/2019-02/1550928122_9k_p_n_2017.jpg)
![ГДЗ Українська мова 8 клас. Підручник [Глазова О.П.] 2021 ГДЗ Українська мова 8 клас. Підручник [Глазова О.П.] 2021](/uploads/posts/2021-10/1633720388_8k_y_g_2021.jpg)
![ГДЗ Вступ до історії 5 клас. Підручник [Гісем О.В.] 2018 ГДЗ Вступ до історії 5 клас. Підручник [Гісем О.В.] 2018](/uploads/posts/2019-07/1564163269_5k_i_h_2018.jpg)