ГДЗ Геометрія 8 клас. Підручник [Істер О.С.] 2021

1061. У п’ятикутнику ABCDE всі кути однакові та всі сторони між собою рівні. Діагоналі AD і BE перетинаються в точці O. Доведіть, що AAED v AAOE.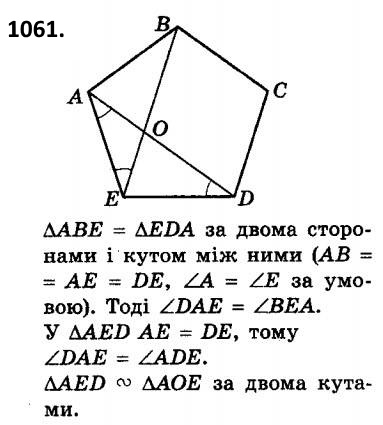 
1062. Через вершину A паралелограма ABCD проведено пряму, яка перетинає продовження сторін CB і CD відповідно в точках N і M. Доведіть, що добуток BN * DM не залежить від того, як проведено цю пряму. 
1063. Діагональ трапеції ділить її на два подібних трикутники. Визначте довжину цієї діагоналі, якщо основи трапеції дорівнюють а і b.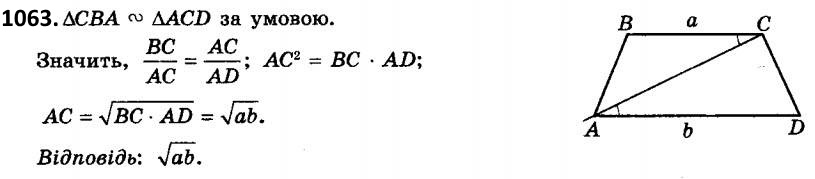 
1064. Через середину найбільшої сторони трикутника проведено пряму, яка відтинає від нього трикутник, подібний даному. Знайдіть найменшу сторону трикутника, що відтинається, якщо сторони даного дорівнюють: 1) 42 см; 49 см; 56 см; 2) 42 см; 49 см; 63 см; 3) 42 см; 49 см; 70 см. Скільки розв’язків має задача в кожному з випадків? 
1065. У трикутнику ABC кут B - тупий. Позначте на стороні AC таку точку D, щоб виконувалася рівність AB2 =AD * AC
1066. AD і BC — основи трапеції ABCD. Діагоналі трапеції взаємно перпендикулярні. AC = 15 см, CE - висота трапеції, AE = 9 см. Знайдіть середню лінію трапеції.

---

---

Назад

Вперед

1 ... 51 52 53 54 55 56 57 58 59 ... 67

ГДЗ 2021 Геометрія Істер Підручник 8 клас Генеза