ГДЗ Геометрія 8 клас. Підручник [Істер О.С.] 2021

1075. Чи існує многокутник, у якого: 1) 20 діагоналей; 2) 21 діагональ?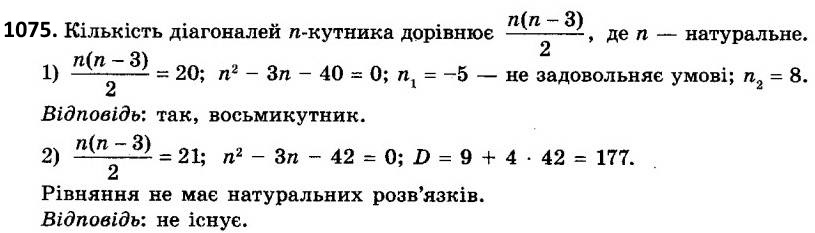 
1076. В опуклому n-кутнику п’ять кутів мають градусну міру 140° кожний, інші кути - гострі. Знайдіть n. 
1077. Доведіть, що відстані від довільної точки діагоналі паралелограма до непаралельних сторін обернено пропорційні довжинам цих сторін.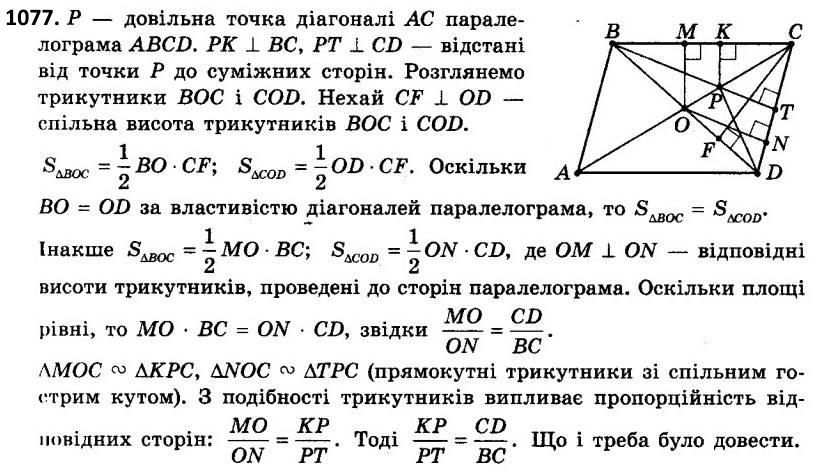
1078. Усередині прямокутного трикутника ABC (ZC = 90°) узято точку M так, що площі трикутників AMB, BMC і CMA рівні між собою. Доведіть, що MA2 + MB2 = 5MC2. 
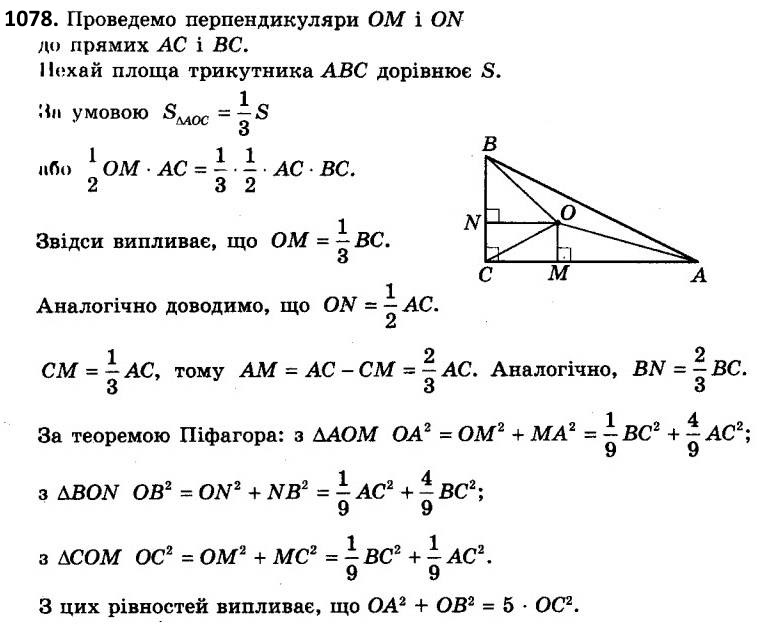1079. У скільки разів площа трикутника ABC більша за площу трикутника ABM, де M - точка перетину медіан трикутника ABC? 
1080. У трикутнику ABC h1, h2, h3 - висоти, проведені відповідно до сторін AB, BC і CA, а d1, d2, d3 - відстані від довільної точки P, що міститься всередині цього трикутника, до сторін AB, BC і CA відповідно.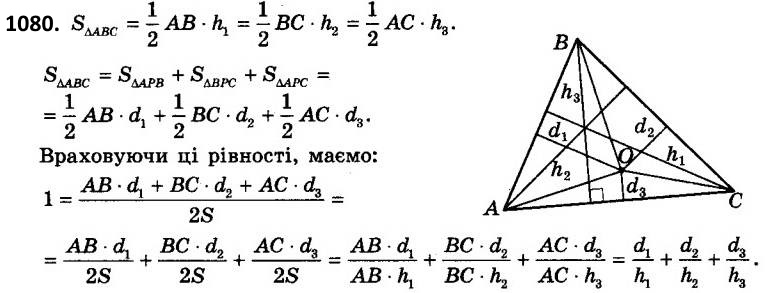 
1081. Точка перетину бісектрис трикутника на 3 см віддалена від прямої, що містить одну зі сторін трикутника. Знайдіть площу трикутника, якщо його периметр дорівнює 36 см. 
1082. На сторонах AB, BC, AC трикутника ABC позначено точки M, K, P так, що AM : MB = BK : KC = CP : PA = 2 : 1. Площа трикутника ABC дорівнює S. Знайдіть площу чотирикутника APKM.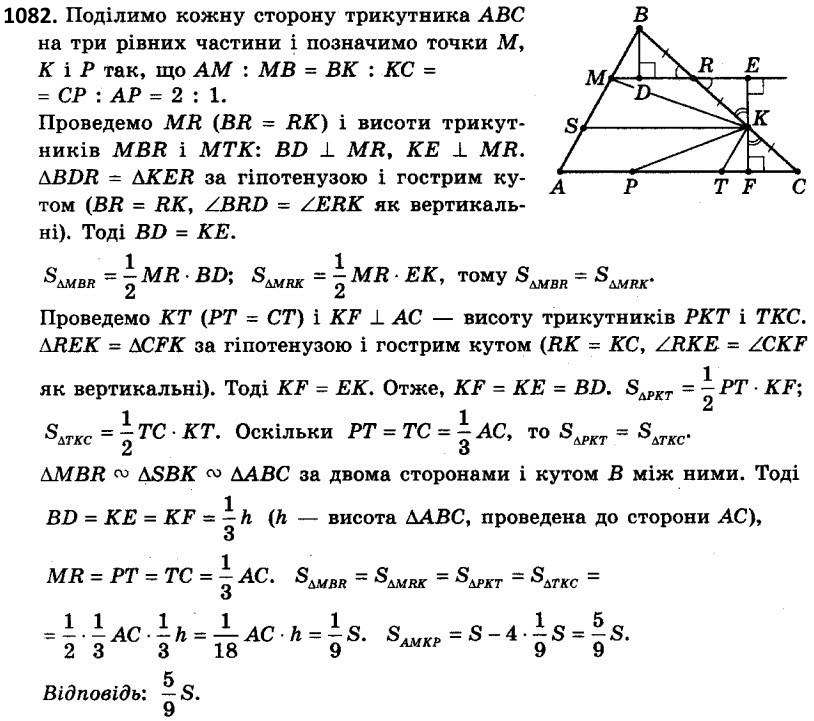 
1083. Бісектриси всіх кутів трапеції перетинаються в точці O, яка міститься на відстані d від більшої сторони трапеції. Знайдіть площу трапеції, якщо її бічні сторони дорівнюють m і n. 
1084. AD і BC - основи трапеції ABCD, CD = c. Точка K - середина бічної сторони AB. Відстань від точки K до прямої, що містить сторону CD, дорівнює d. Знайдіть площу трапеції. 
1085. У трапеції ABCD M - середина більшої основи AD, AB = BC = CD = a. Точка перетину діагоналей трапеції збігається з точкою перетину висот трикутника BMC. Знайдіть площу трапеції.

---

---

Назад

Вперед

1 ... 53 54 55 56 57 58 59 60 61 ... 67

ГДЗ 2021 Геометрія Істер Підручник 8 клас Генеза