ГДЗ Геометрія 8 клас. Підручник [Істер О.С.] 2021

1067. Діагоналі чотирикутникаABCD взаємно перпендикулярні. Доведіть, що AD2 + BC2 = AB2 + CD2.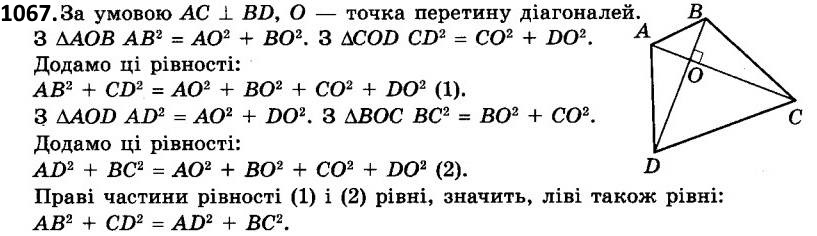 
1068. Точка M лежить усередині кута, який дорівнює 60°. Відстані від точки M до сторін кута дорівнюють а і b. Знайдіть відстань від точки M до вершини кута. 
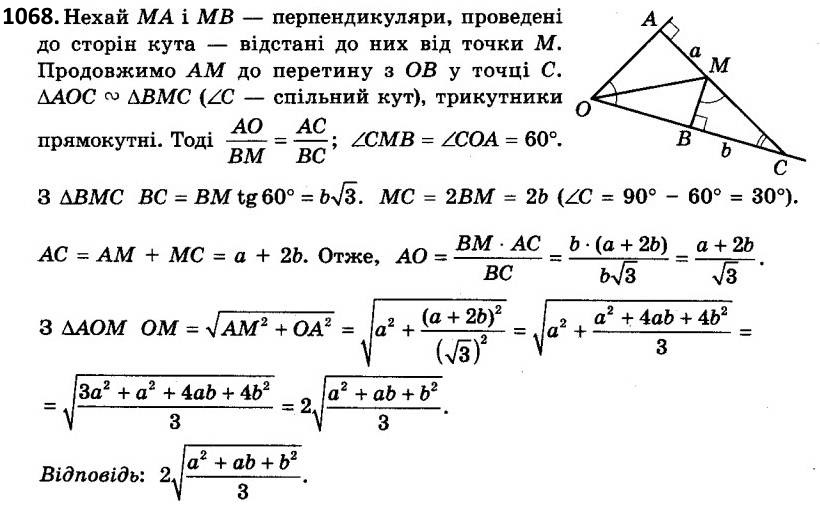1069. Два кола різних радіусів мають зовнішній дотик. MN - їхня спільна зовнішня дотична, M і N - точки дотику. Доведіть, що довжина відрізка MN є середнім геометричним діаметрів кіл. 
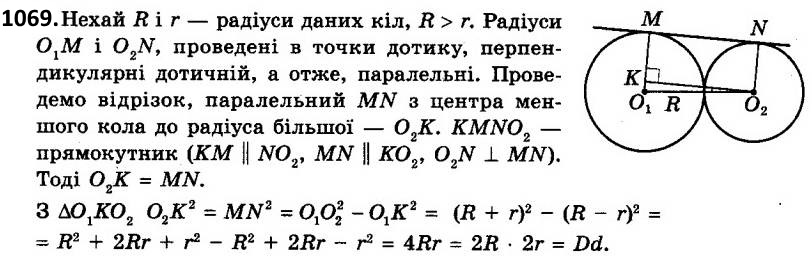1070. 1) У гострокутному трикутнику ABC BH - висота. Доведіть, що BC2 = AB2 + AC2 - 2AC • AH. 2) У трикутникуABC ZA - тупий, BH - висота. Доведіть, що BC2 = AB2 + AC2 + 2AC • AH. 
1071. У прямокутний трикутник вписано коло. Точка дотику ділить гіпотенузу у відношенні 2 : 3. Знайдіть периметр трикутника, якщо центр вписаного кола міститься на відстані m\/2 від вершини прямого кута. 
1072. Нехай а і b - катети прямокутного трикутника, c - його гіпотенуза, h - висота, проведена до гіпотенузи. Доведіть, що трикутник зі сторонами h, c + h і а + b - прямокутний.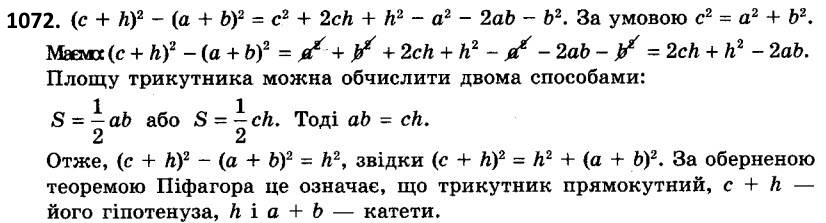 
1073. ABCD - прямокутна трапеція, ZA = ZB = 90°, AB = а, CD = b, BC = c, BC < DA. Знайдіть відстань від точки B до прямої, що містить CD. 
1074. Обчисліть: 1) sin 15°; 2) sin 75°.

---

---

Назад

Вперед

1 ... 52 53 54 55 56 57 58 59 60 ... 67

ГДЗ 2021 Геометрія Істер Підручник 8 клас Генеза