ГДЗ Геометрія 8 клас. Підручник [Мерзляк А.Г., Полонський В.Б., Якір М.С.] 2021

278. Чому дорівнює градусна міра центрального кута кола, який спирається на дугу, що становить:
1) 1/6 кола;
2) 1/10 кола;
3) 1/2 кола;
4) 2/9 кола?
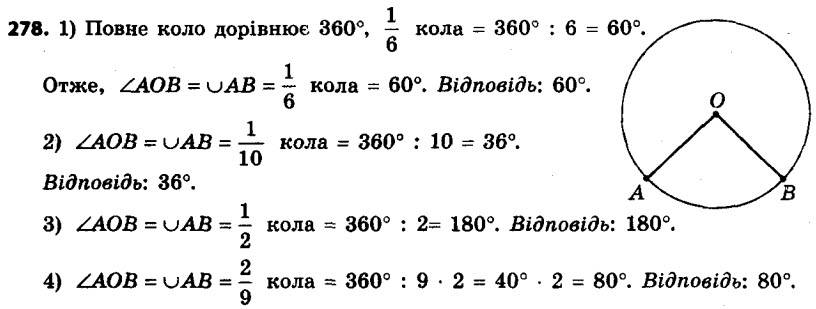279. Знайдіть градусні міри двох дуг кола, на які його ділять дві точки, якщо градусна міра однієї з дуг на 80° більша за градусну міру другої.
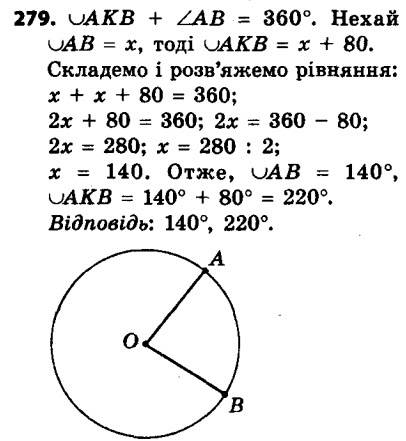280. Знайдіть градусні міри двох дуг кола, на які його ділять дві точки, якщо градусні міри цих дуг відносяться як 7 : 11.
281. Знайдіть градусну міру дуги, яку описує кінець годинної стрілки:
1) за 2 год;
2) за 5 год;
3) за 8 год;
4) за 30 хв;
5) за 12 год.
282. Які з кутів, зображених на рисунку 90, є вписаними? На яку дугу спирається кожний із вписаних кутів?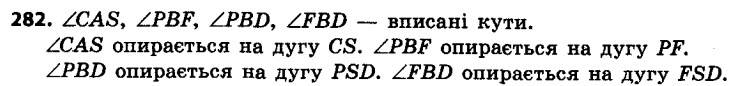
283. На рисунку 91 зображено коло із центром O. Знайдіть:
1) кут BDC, якщо ∠BAC = 40°;
2) кут BEC, якщо ∠BOC = 70°;
3) дугу CE, якщо ∠CDE = 80°;
4) дугу DBA, якщо ∪DBA = 300°
284. Знайдіть помилки на рисунку 92.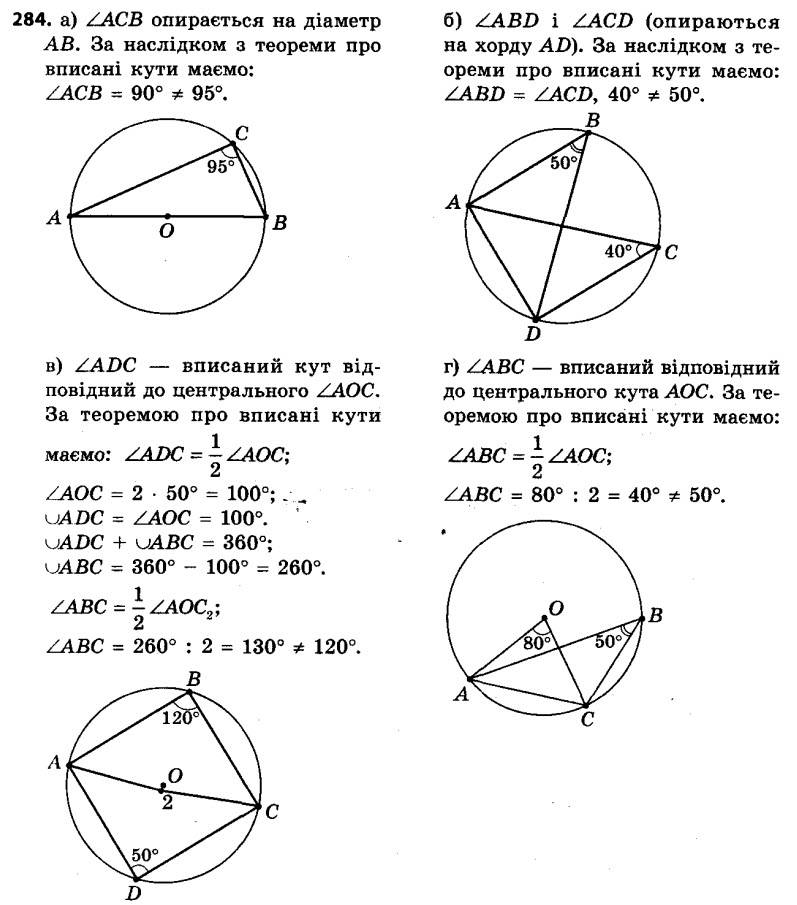
285. Знайдіть вписаний кут, якщо градусна міра дуги, на яку він спирається, дорівнює:
1) 84°;
2) 110°;
3) 230°;
4) 340°.
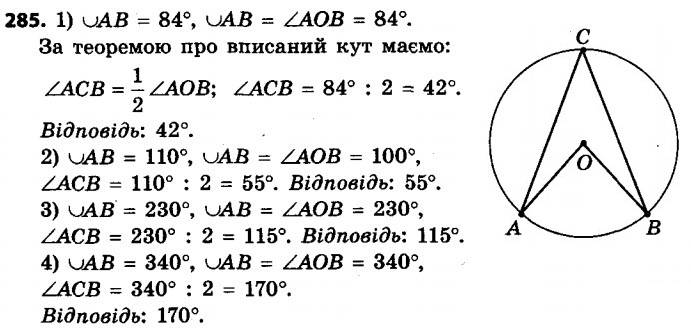286. На рисунку 93 ∪AB = 74°, ∠ABC = 68°. Знайдіть дугу BC.

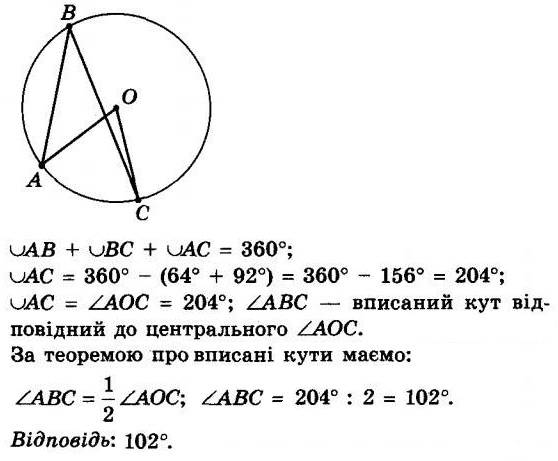288. Центральний кут AOC на 25° більший за вписаний кут ABC, що спирається на дугу AС (рис. 94). Знайдіть кути AOC і ABC.
289. Кінці хорди AB ділять коло на дві дуги, градусні міри яких відносяться як 3 : 7. Під якими кутами видно цю хорду з точок M і K (рис. 95)?
290. На рисунку 96 хорди AB і CD рівні. Доведіть, що ∪AMB = ∪CND.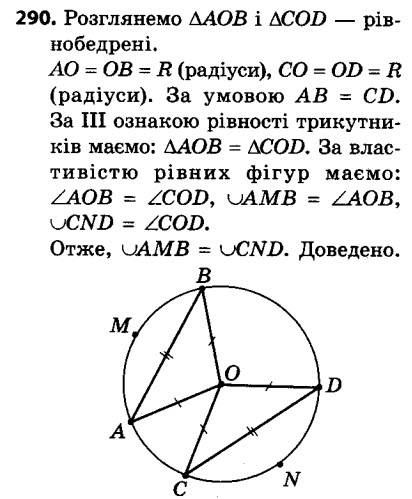
291. Доведіть, що коли дві дуги кола рівні, то рівні й хорди, які їх стягують.
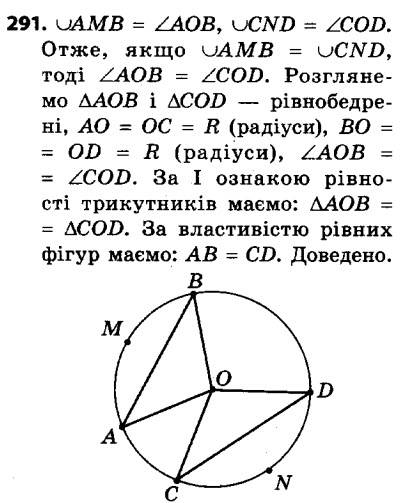292. Точки A, B і C ділять коло на три дуги так, що ∪AB : ∪BC : ∪AC = 1 : 2 : 3. Знайдіть кути трикутника ABC.
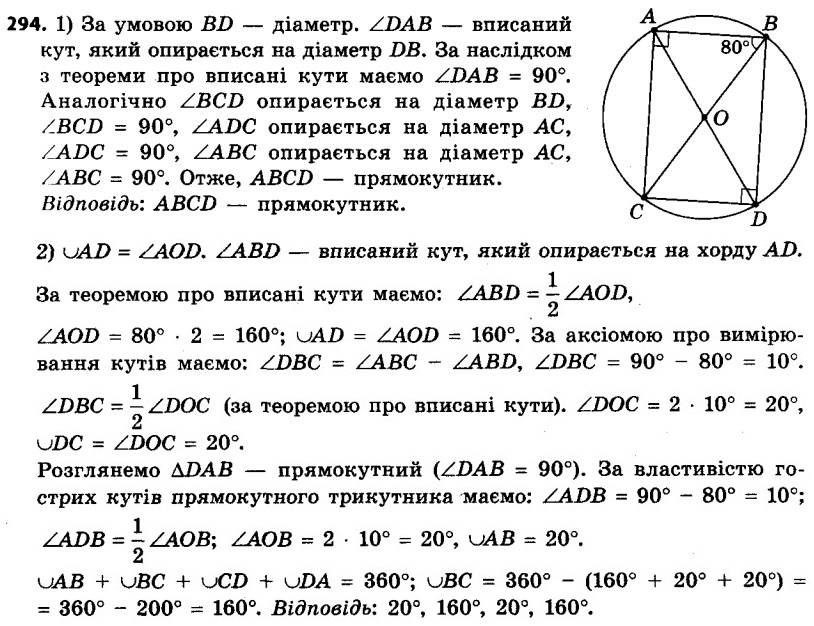
293. Вершини рівнобедреного трикутника ABC (AB = BC) ділять описане навколо нього коло на три дуги, причому ∪AB = 70°. Знайдіть кути трикутника ABC.
294. Кінці діаметрів AC і BD кола послідовно сполучили так, що утворився чотирикутник ABCD.
1) Визначте вид чотирикутника ABCD.
2) Знайдіть дуги AB, BC, CD і AD, якщо ∠ABD = 80°.
295. Гострий кут прямокутного трикутника дорівнює 32°. Знайдіть градусні міри дуг, на які вершини трикутника ділять коло, описане навколо нього, та радіус цього кола, якщо гіпотенуза даного трикутника дорівнює 12 см.
296. Доведіть, що коли вписаний кут є прямим, то він спирається на діаметр.
297. Хорди AB і CD кола перетинаються в точці M (рис. 97). Доведіть, що ∠AMC = 1 2 (∪AC + ∪BD).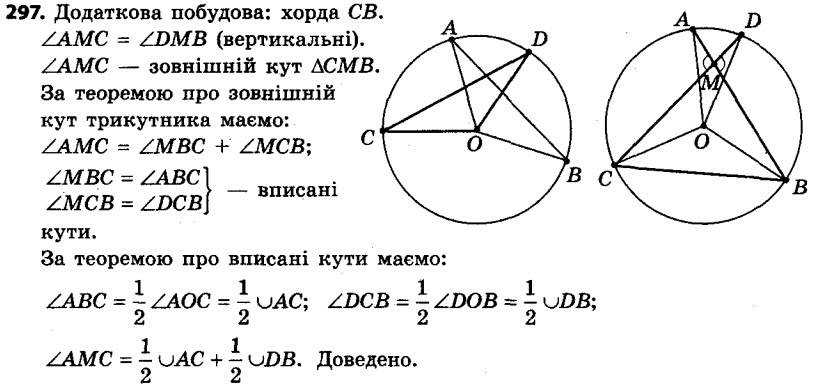
298. Хорди AB і CD кола не перетинаються, а прямі AB і CD перетинаються в точці M (рис. 98). Доведіть, що ∠AMC = 1/2 (∪AC – ∪BD).
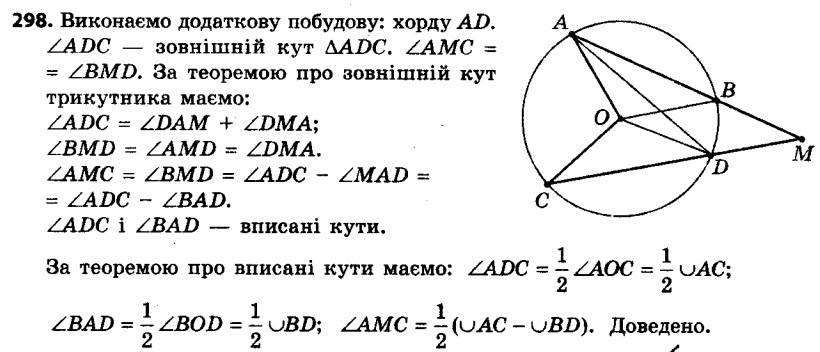299. Через точку A, яка лежить поза колом із центром O, проведено дві прямі, одна з яких дотикається до кола в точці B, а друга проходить через його центр (рис. 99). Відомо, що ∪BMC = 100°. Знайдіть кут BAC.
300. Бісектриса кута B трикутника ABC перетинає коло, описане навколо цього трикутника, у точці D. Знайдіть кути трикутника ADC, якщо ∠ABC = 80°.
301. На дузі AC кола, описаного навколо рівностороннього трикутника ABC, позначено точку M так, що ∪AM = 2 ∪CM. Знайдіть кути трикутника AMC.
302. Коло, побудоване на стороні AB трикутника ABC як на діаметрі, перетинає сторони AC і BC у точках M і K відповідно. Доведіть, що відрізки AK і BM — висоти трикутника ABC.
303. Коло, побудоване на стороні AC трикутника ABC як на діаметрі, перетинає сторону AB у точці K так, що ∠ACK = ∠BCK. Доведіть, що трикутник ABC рівнобедрений.
304. Доведіть, що градусні міри дуг кола, які містяться між двома паралельними хордами, рівні.
305. Вершини квадрата ABCD лежать на колі. На дузі AB позначено довільну точку M. Доведіть, що ∠AMD = ∠CMD = ∠CMB.
306. Кут при вершині рівнобедреного трикутника дорівнює 56°. На бічній стороні трикутника як на діаметрі побудовано півколо, яке інші сторони трикутника ділять на три дуги. Знайдіть градусні міри утворених дуг.
307. Як, користуючись лише косинцем, знайти центр даного кола?
308. Дано коло, у якому проведено діаметр AB, і позначено точку C поза колом (рис. 100). Як, користуючись лише лінійкою, провести через точку C пряму, що перпендикулярна до прямої AB?
309. Два кола мають єдину спільну точку M. Через точку M проведено дві прямі, які перетинають дані кола. Точки їхнього перетину з колами, відмінні від точки M, сполучено хордами. Доведіть, що ці хорди паралельні.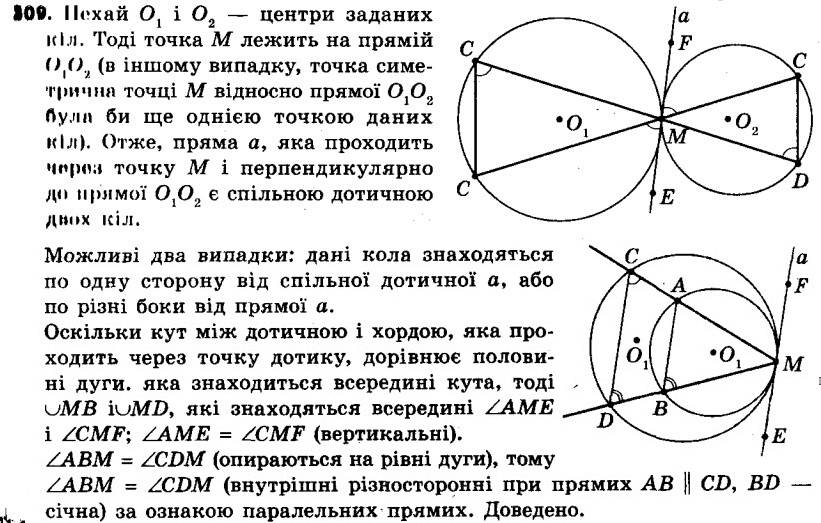
310. До кола, описаного навколо трикутника ABC, проведено в точці B дотичну, яка перетинає пряму AC у точці D. Відрізок BM — бісектриса трикутника ABC. Доведіть, що BD = MD
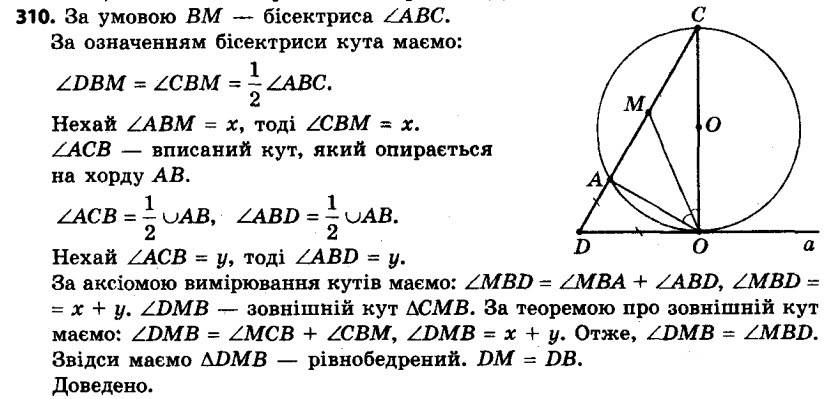311. Дано відрізок AB і кут a. Знайдіть геометричне місце точок X таких, що ∠AXB = a.
312. Побудуйте трикутник за стороною, протилежним їй кутом і висотою, проведеною до даної сторони.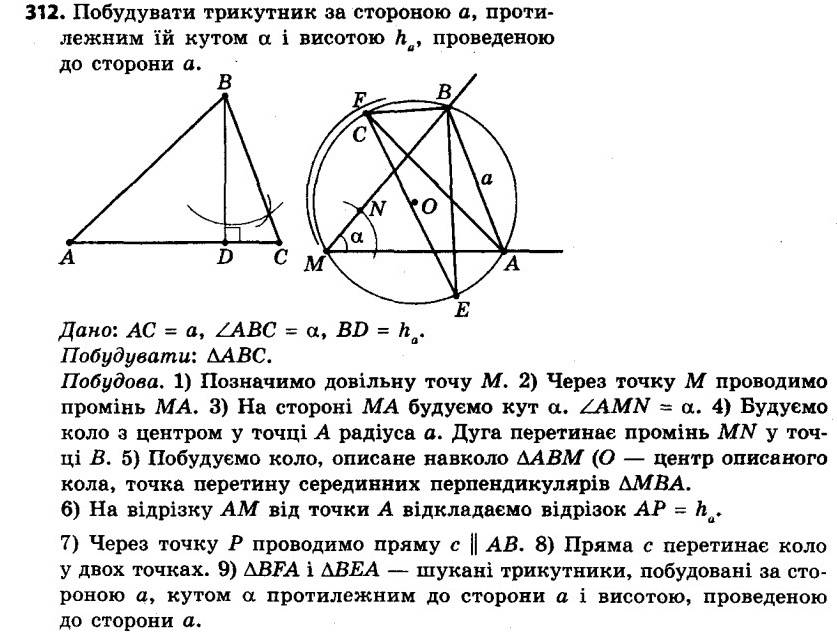
313. Побудуйте трикутник за стороною, протилежним їй кутом і медіаною, проведеною до даної сторони.
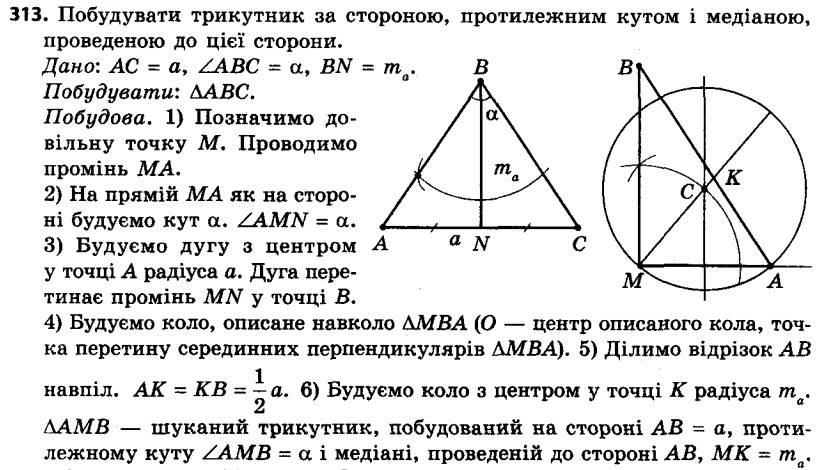314. Побудуйте паралелограм за двома сторонами та кутом між діагоналями.
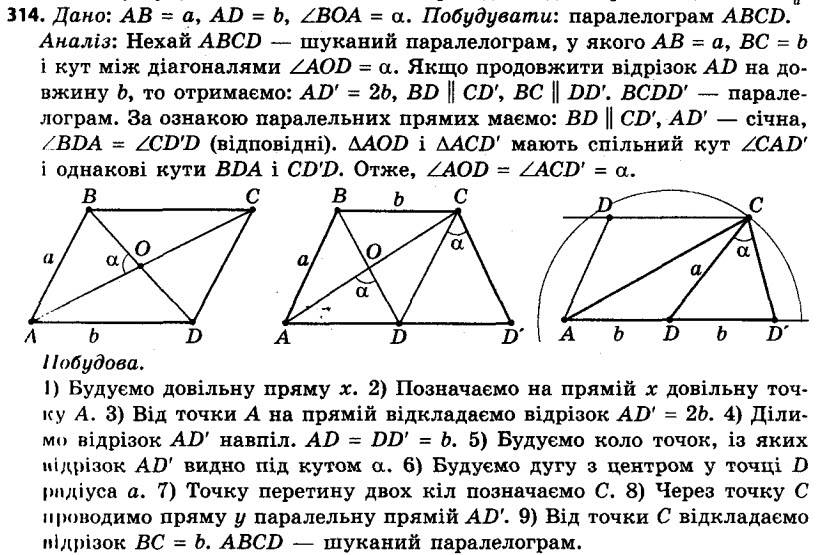315. Побудуйте паралелограм за кутом і двома діагоналями.
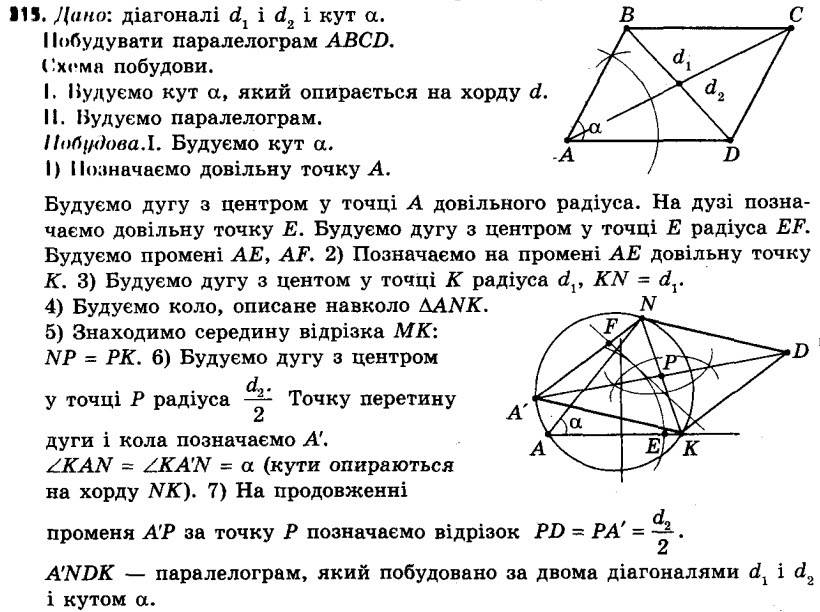316. У прямокутному трикутнику АВС на катеті АС як на діаметрі побудовано коло, що перетинає гіпотенузу АВ у точці Е. Через точку Е проведено дотичну до кола, яка перетинає катет СВ у точці D. Доведіть, що трикутник ВDE рівнобедрений.
317. Дано відрізок AB. Знайдіть геометричне місце точок X таких, що трикутник AXB прямокутний.
318. Бісектриса кута A трикутника ABC перетинає описане навколо нього коло в точці D. Точка O — центр вписаного кола трикутника ABC. Доведіть, що DO = DB = DC.
319. Бісектриси кутів A, B і C трикутника ABC перетинають описане навколо нього коло в точках A1, B1 і C1 відповідно. Доведіть, що A1B1 ^ CC1.
320. На рисунку 101 зображено два кола із центрами O1 і O2. Побудуйте пряму l, яка дотикається до цих кіл так, що точки дотику лежать в одній півплощині відносно прямої O1O2 (таку пряму називають зовнішньою спільною дотичною до двох даних кіл).
321. Побудуйте трикутник:
1) за стороною, протилежним їй кутом і радіусом вписаного кола;
2) за стороною, протилежним їй кутом і медіаною, проведеною до другої сторони.
322. Периметр трикутника ABC дорівнює 30 см. Точка дотику вписаного кола до сторони AB ділить її у відношенні 3 : 2, рахуючи від вершини A, а точка дотику до сторони BC віддалена від вершини С на 5 см. Знайдіть сторони трикутника.
323. До кола, вписаного в трикутник ABC, проведено три дотичні (рис. 102). Периметри трикутників, які ці дотичні відтинають від даного трикутника, дорівнюють P1, P2 і P3. Знайдіть периметр трикутника ABC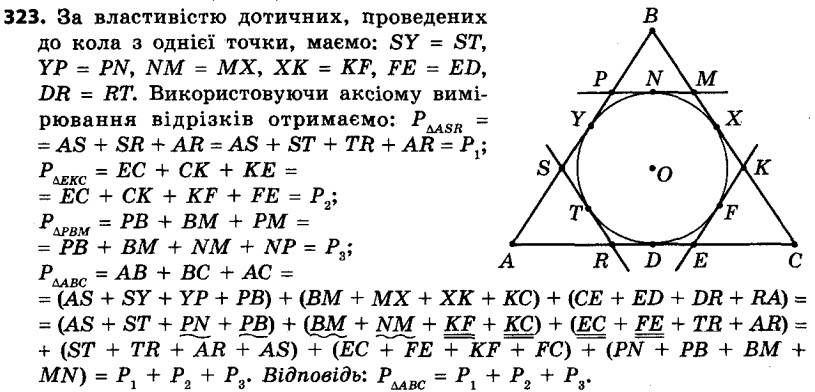
324. Установіть вид трикутника, у якого центр описаного кола належить медіані.
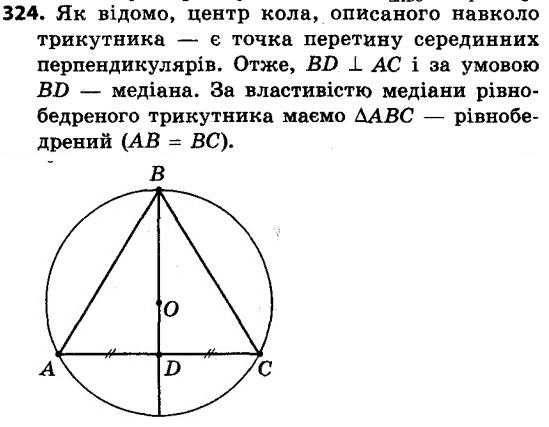325. Клітинки квадрата розміром 100 × 100 клітинок розфарбовано в шаховому порядку. Квадрат розрізали на квадрати, сторони яких містять непарну кількість клітинок, і в кожному такому квадраті позначили центральну клітинку. Доведіть, що білих і чорних клітинок позначено порівну.

---

---

Назад

Вперед

1 ... 6 7 8 9 10 11 12 13 14 ... 32

ГДЗ 2021 Підручник 8 клас Геометрія Мерзляк Полонський Якір Гімназія