ГДЗ Геометрія 8 клас. Підручник [Мерзляк А.Г., Полонський В.Б., Якір М.С.] 2021
13. Перша ознака подібності трикутників
449. На рисунку 144 ∠BAC = ∠BED. Чи подібні трикутники ABC і EDB? У разі ствердної відповіді вкажіть пари відповідних сторін. 450. На рисунку 145 DE ^ AB, BC ^ AD. Укажіть усі пари подібних трикутників, які зображено на цьому рисунку.
450. На рисунку 145 DE ^ AB, BC ^ AD. Укажіть усі пари подібних трикутників, які зображено на цьому рисунку.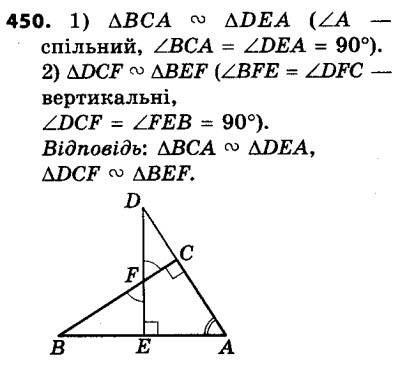 451. На рисунку 146 ∠ABC = ∠BDC. Які трикутники на цьому рисунку подібні? Запишіть рівність відношень їхніх відповідних сторін
451. На рисунку 146 ∠ABC = ∠BDC. Які трикутники на цьому рисунку подібні? Запишіть рівність відношень їхніх відповідних сторін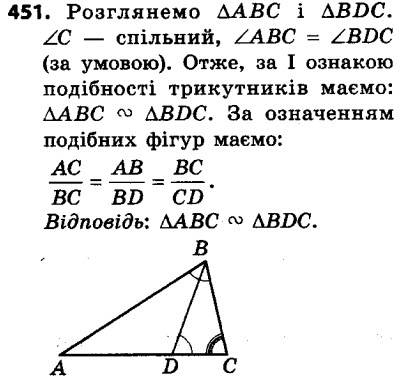 452. Укажіть пари подібних трикутників, зображених на рисунку 147, знайдіть довжину відрізка x (розміри дано в сантиметрах).
452. Укажіть пари подібних трикутників, зображених на рисунку 147, знайдіть довжину відрізка x (розміри дано в сантиметрах).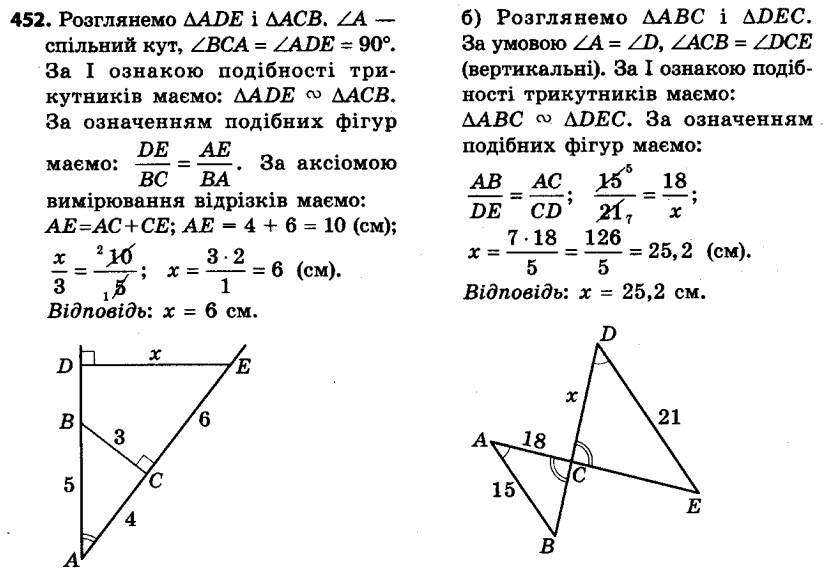 453. У трикутниках ABC і A1B1C1 відомо, що ∠A = ∠A1, ∠B = ∠B1, AB = 6 см, BC = 8 см, A1B1 = 9 см, A1C1 = 18 см. Знайдіть невідомі сторони даних трикутників.
453. У трикутниках ABC і A1B1C1 відомо, що ∠A = ∠A1, ∠B = ∠B1, AB = 6 см, BC = 8 см, A1B1 = 9 см, A1C1 = 18 см. Знайдіть невідомі сторони даних трикутників. 454. На стороні CD паралелограма ABCD (рис. 148) позначено точку E, прямі BE і AD перетинаються в точці F, CE = 8 см, DE = 4 см, BE = 10 см, AD = 9 см. Знайдіть відрізки EF і FD.
454. На стороні CD паралелограма ABCD (рис. 148) позначено точку E, прямі BE і AD перетинаються в точці F, CE = 8 см, DE = 4 см, BE = 10 см, AD = 9 см. Знайдіть відрізки EF і FD. 455. У трапеції ABCD (BC || AD) відомо, що AD = 20 см, BC = 15 см, O — точка перетину діагоналей, AO = 16 см. Знайдіть OC.
455. У трапеції ABCD (BC || AD) відомо, що AD = 20 см, BC = 15 см, O — точка перетину діагоналей, AO = 16 см. Знайдіть OC. 456. Діагоналі трапеції ABCD з основами BC і AD перетинаються в точці O. Знайдіть основу AD, якщо BO : OD = 3 : 7, BC = 18 см.
456. Діагоналі трапеції ABCD з основами BC і AD перетинаються в точці O. Знайдіть основу AD, якщо BO : OD = 3 : 7, BC = 18 см. 457. Чи подібні два прямокутних трикутники, якщо серед кутів одного з них є кут, який дорівнює 38°, а серед кутів другого — кут, який дорівнює 52°?
457. Чи подібні два прямокутних трикутники, якщо серед кутів одного з них є кут, який дорівнює 38°, а серед кутів другого — кут, який дорівнює 52°? 458. Доведіть, що два рівнобедрених трикутники подібні, якщо кути, протилежні їхнім основам, рівні.
458. Доведіть, що два рівнобедрених трикутники подібні, якщо кути, протилежні їхнім основам, рівні. 459. Чи можна стверджувати, що два рівнобедрених трикутники подібні, якщо в них є:
459. Чи можна стверджувати, що два рівнобедрених трикутники подібні, якщо в них є:1) по рівному гострому куту;
2) по прямому куту;
3) по рівному тупому куту?
 460. Кут між бічною стороною та основою одного рівнобедреного трикутника дорівнює куту між бічною стороною та основою другого рівнобедреного трикутника. Бічна сторона та основа першого трикутника дорівнюють 18 см і 10 см відповідно, а основа другого — 8 см. Знайдіть бічну сторону другого трикутника.
460. Кут між бічною стороною та основою одного рівнобедреного трикутника дорівнює куту між бічною стороною та основою другого рівнобедреного трикутника. Бічна сторона та основа першого трикутника дорівнюють 18 см і 10 см відповідно, а основа другого — 8 см. Знайдіть бічну сторону другого трикутника. 461. Із вершини прямого кута трикутника опущено висоту на гіпотенузу. Скільки подібних трикутників утворилося при цьому?
461. Із вершини прямого кута трикутника опущено висоту на гіпотенузу. Скільки подібних трикутників утворилося при цьому? 462. Сторони паралелограма дорівнюють 20 см і 14 см, висота, проведена до більшої сторони, дорівнює 7 см. Знайдіть висоту паралелограма, проведену до меншої сторони.
462. Сторони паралелограма дорівнюють 20 см і 14 см, висота, проведена до більшої сторони, дорівнює 7 см. Знайдіть висоту паралелограма, проведену до меншої сторони. 463. У трапеції ABCD з основами BC і AD діагоналі перетинаються в точці O, BO = 4 см, OD = 20 см, AC = 36 см. Знайдіть відрізки AO і OC.
463. У трапеції ABCD з основами BC і AD діагоналі перетинаються в точці O, BO = 4 см, OD = 20 см, AC = 36 см. Знайдіть відрізки AO і OC. 464. У трапеції ABCD (BC || AD) відомо, що AD = 18 см, BC = 14 см, AC = 24 см. Знайдіть відрізки, на які точка перетину діагоналей ділить діагональ AC.
464. У трапеції ABCD (BC || AD) відомо, що AD = 18 см, BC = 14 см, AC = 24 см. Знайдіть відрізки, на які точка перетину діагоналей ділить діагональ AC. 465. Доведіть, що в подібних трикутниках бісектриси, проведені з вершин відповідних кутів, відносяться як відповідні сторони.
465. Доведіть, що в подібних трикутниках бісектриси, проведені з вершин відповідних кутів, відносяться як відповідні сторони.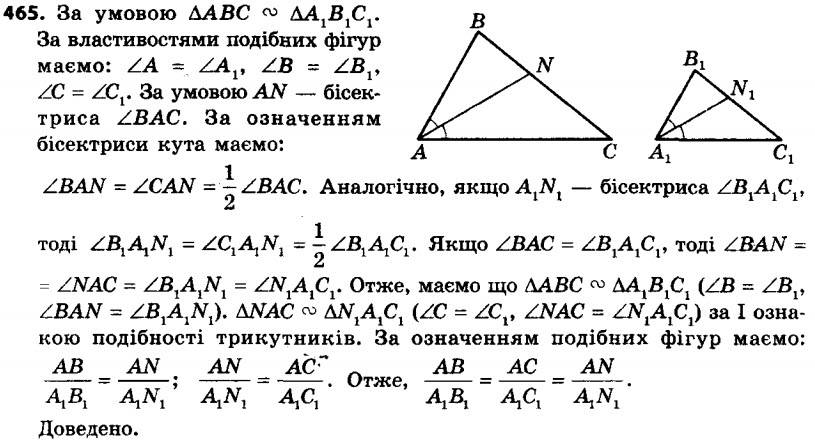 466. Доведіть, що в подібних трикутниках висоти, проведені з вершин відповідних кутів, відносяться як відповідні сторони.
466. Доведіть, що в подібних трикутниках висоти, проведені з вершин відповідних кутів, відносяться як відповідні сторони.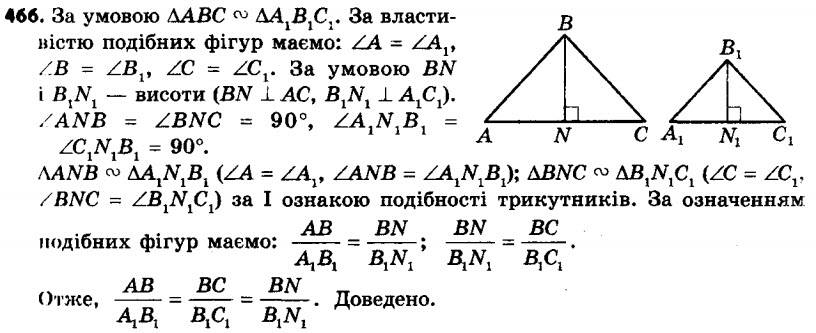 467. Основи BC і AD трапеції ABCD дорівнюють відповідно 28 см і 63 см, ∠ABC = = ∠ACD. Знайдіть діагональ AC.
467. Основи BC і AD трапеції ABCD дорівнюють відповідно 28 см і 63 см, ∠ABC = = ∠ACD. Знайдіть діагональ AC. 468. На стороні AC трикутника ABC позначили точку D таку, що ∠ABD = ∠C, AB = 20 см, BC = 28 см, AC = 40 см. Знайдіть невідомі сторони трикутника ABD
468. На стороні AC трикутника ABC позначили точку D таку, що ∠ABD = ∠C, AB = 20 см, BC = 28 см, AC = 40 см. Знайдіть невідомі сторони трикутника ABD 469. Гіпотенуза прямокутного трикутника дорівнює 20 см, а більший катет — 16 см. Знайдіть відрізки, на які серединний перпендикуляр гіпотенузи ділить більший катет.
469. Гіпотенуза прямокутного трикутника дорівнює 20 см, а більший катет — 16 см. Знайдіть відрізки, на які серединний перпендикуляр гіпотенузи ділить більший катет. 470. Поясніть за допомогою рисунка 149, як можна знайти ширину BM річки, використовуючи подібність трикутників.
470. Поясніть за допомогою рисунка 149, як можна знайти ширину BM річки, використовуючи подібність трикутників. 471. Зображення дерева, віддаленого на 60 м від об’єктива фотоапарата, має на плівці висоту 8 мм (рис. 150). Відстань від об’єктива до зображення дорівнює 40 мм. Яка висота дерева?
471. Зображення дерева, віддаленого на 60 м від об’єктива фотоапарата, має на плівці висоту 8 мм (рис. 150). Відстань від об’єктива до зображення дорівнює 40 мм. Яка висота дерева? 472. Знайдіть висоту дерева, якщо довжина його тіні дорівнює 8,4 м, а довжина тіні від вертикального стовпа заввишки 2 м у той самий час доби дорівнює 2,4 м (рис. 151).
472. Знайдіть висоту дерева, якщо довжина його тіні дорівнює 8,4 м, а довжина тіні від вертикального стовпа заввишки 2 м у той самий час доби дорівнює 2,4 м (рис. 151). 473. Чи може пряма перетинати дві сторони рівнобедреного трикутника, відтинаючи від нього трикутник, йому подібний, і не бути паралельною третій стороні?
473. Чи може пряма перетинати дві сторони рівнобедреного трикутника, відтинаючи від нього трикутник, йому подібний, і не бути паралельною третій стороні?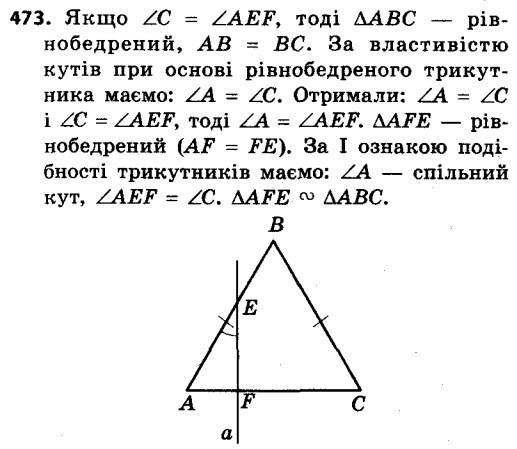 474. Хорди AB і CD кола перетинаються в точці M, AM = 6 см, BM = 14 см, CM = 12 см. Знайдіть відрізок DM.
474. Хорди AB і CD кола перетинаються в точці M, AM = 6 см, BM = 14 см, CM = 12 см. Знайдіть відрізок DM.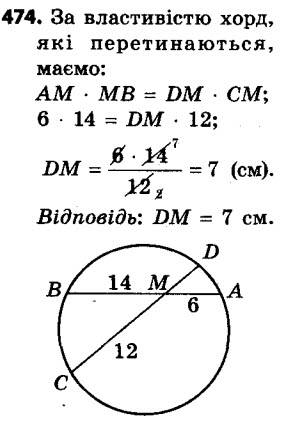 475. Хорди MK і NP кола перетинаються в точці F, MF = 9 см, KF = 12 см, а відрізок NF у 3 рази довший за відрізок PF. Знайдіть довжину хорди NP.
475. Хорди MK і NP кола перетинаються в точці F, MF = 9 см, KF = 12 см, а відрізок NF у 3 рази довший за відрізок PF. Знайдіть довжину хорди NP.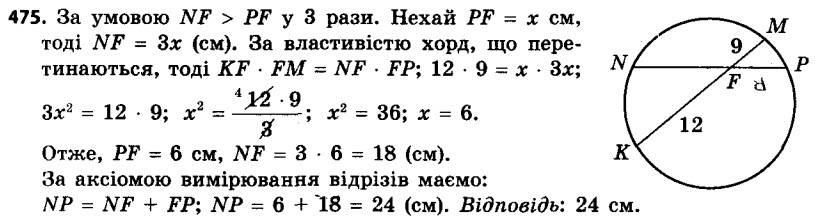 476. Точка K ділить хорду AC кола навпіл, а хорду DE — на відрізки завдовжки 2 см і 32 см. Знайдіть довжину хорди AC.
476. Точка K ділить хорду AC кола навпіл, а хорду DE — на відрізки завдовжки 2 см і 32 см. Знайдіть довжину хорди AC. 477. Точка E ділить хорду CD кола на відрізки завдовжки 15 см і 16 см. Знайдіть радіус кола, якщо відстань від точки E до центра кола дорівнює 4 см.
477. Точка E ділить хорду CD кола на відрізки завдовжки 15 см і 16 см. Знайдіть радіус кола, якщо відстань від точки E до центра кола дорівнює 4 см. 478. Точка P ділить хорду MK кола на два відрізки завдовжки 8 см і 12 см. Знайдіть відстань від точки P до центра кола, якщо його радіус дорівнює 11 см.
478. Точка P ділить хорду MK кола на два відрізки завдовжки 8 см і 12 см. Знайдіть відстань від точки P до центра кола, якщо його радіус дорівнює 11 см. 479. Через точку A проведено до кола дотичну AM (M — точка дотику) і січну, яка перетинає коло в точках K і P (точка K лежить між точками A і P). Знайдіть відрізок KP, якщо AM = 12 см, AP = 18 см.
479. Через точку A проведено до кола дотичну AM (M — точка дотику) і січну, яка перетинає коло в точках K і P (точка K лежить між точками A і P). Знайдіть відрізок KP, якщо AM = 12 см, AP = 18 см. 480. Через точку A, яка лежить поза колом, проведено дві прямі, одна з яких дотикається до кола в точці B, а друга перетинає коло в точках C і D (точка C лежить між точками A і D), AB = 18 см, AC : CD = 4 : 5. Знайдіть відрізок AD.
480. Через точку A, яка лежить поза колом, проведено дві прямі, одна з яких дотикається до кола в точці B, а друга перетинає коло в точках C і D (точка C лежить між точками A і D), AB = 18 см, AC : CD = 4 : 5. Знайдіть відрізок AD.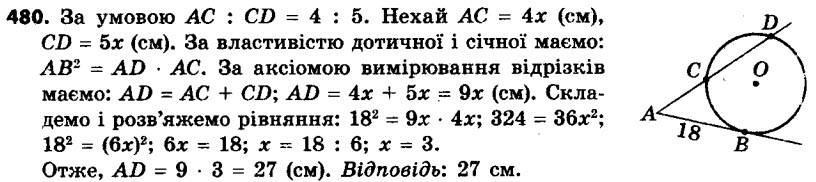
481. Через точку A, що лежить поза колом (рис. 152), проведено дві прямі, одна з яких перетинає коло в точках B і C (точка B лежить між точками A і C), а друга — у точках D і E (точка D лежить між точками A і E).
1) Доведіть, що ABæAC = ADæAE.
2) Знайдіть відрізок AE, якщо AB = 18 см, BC = 12 см і AD : DE = 5 : 7.
 482. У колі, радіус якого дорівнює 8 см, проведено хорду AB. На прямій AB поза відрізком AB позначили точку C таку, що AC : BC = 1 : 4. Знайдіть відстань від точки C до центра кола, якщо AB = 9 см.
482. У колі, радіус якого дорівнює 8 см, проведено хорду AB. На прямій AB поза відрізком AB позначили точку C таку, що AC : BC = 1 : 4. Знайдіть відстань від точки C до центра кола, якщо AB = 9 см. 483. У трикутник ABC вписано квадрат так, що дві його сусідні вершини належать стороні AC, а дві інші — сторонам AB і BC відповідно. Знайдіть сторону квадрата, якщо AC = a, а висота, проведена до сторони AC, дорівнює h.
483. У трикутник ABC вписано квадрат так, що дві його сусідні вершини належать стороні AC, а дві інші — сторонам AB і BC відповідно. Знайдіть сторону квадрата, якщо AC = a, а висота, проведена до сторони AC, дорівнює h. 484. У трикутнику ABC відомо, що BC = 72 см, AD — висота, AD = 24 см. У даний трикутник вписано прямокутник MNKP так, що вершини M і P належать стороні BC, а вершини N і K — сторонам AB і AC відповідно. Знайдіть сторони прямокутника, якщо MP : MN = 9 : 5.
484. У трикутнику ABC відомо, що BC = 72 см, AD — висота, AD = 24 см. У даний трикутник вписано прямокутник MNKP так, що вершини M і P належать стороні BC, а вершини N і K — сторонам AB і AC відповідно. Знайдіть сторони прямокутника, якщо MP : MN = 9 : 5. 485. Знайдіть кути паралелограма, якщо кут між його висотами, проведеними з однієї вершини, дорівнює: 1) 20°; 2) 130°.
485. Знайдіть кути паралелограма, якщо кут між його висотами, проведеними з однієї вершини, дорівнює: 1) 20°; 2) 130°. 486. Два кола із центрами O1 і O2, радіуси яких рівні, перетинаються в точках A і B. Відрізок O1O2 перетинає дані кола в точках C і D. Доведіть, що чотирикутник ACBD — ромб.
486. Два кола із центрами O1 і O2, радіуси яких рівні, перетинаються в точках A і B. Відрізок O1O2 перетинає дані кола в точках C і D. Доведіть, що чотирикутник ACBD — ромб.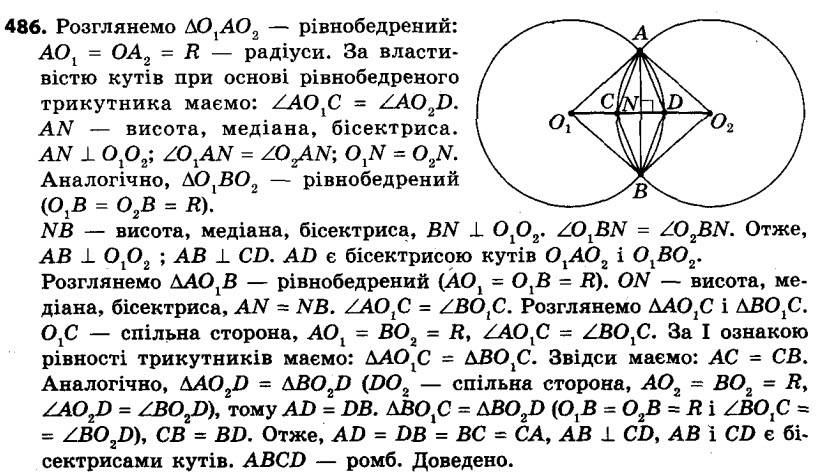 487. Один із кутів прямокутної трапеції дорівнює 135°, середня лінія — 21 см, а основи відносяться як 5 : 2. Знайдіть меншу бічну сторону трапеції.
487. Один із кутів прямокутної трапеції дорівнює 135°, середня лінія — 21 см, а основи відносяться як 5 : 2. Знайдіть меншу бічну сторону трапеції. 488. Як два рівних опуклих чотирикутники розрізати на частини, з яких можна скласти паралелограм?
488. Як два рівних опуклих чотирикутники розрізати на частини, з яких можна скласти паралелограм?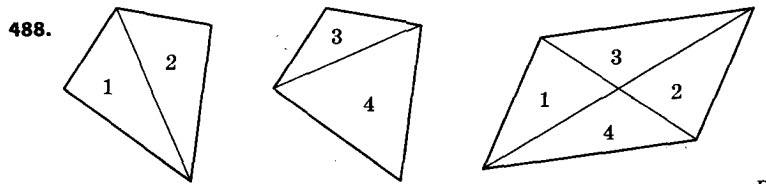
 ГДЗ 2021 Підручник 8 клас Геометрія Мерзляк Полонський Якір Гімназія
ГДЗ 2021 Підручник 8 клас Геометрія Мерзляк Полонський Якір Гімназія
 Якщо помітили в тексті помилку, виділіть її та натисніть Ctrl + Enter
Якщо помітили в тексті помилку, виділіть її та натисніть Ctrl + Enter 15.10.2021,
15.10.2021,
 31 565,
31 565,
 0
0
 Назад
Назад




![ГДЗ Природознавство 5 клас. Підручник [Ярошенко О.Г., Бойко В.М.] 2018 ГДЗ Природознавство 5 клас. Підручник [Ярошенко О.Г., Бойко В.М.] 2018](/uploads/posts/2019-04/1555779316_5_p_y_u2018.jpg)
![ГДЗ Основи правознавства 9 клас. Підручник [Наровлянський О. Д.] 2017 ГДЗ Основи правознавства 9 клас. Підручник [Наровлянський О. Д.] 2017](/uploads/posts/2019-02/1550928122_9k_p_n_2017.jpg)
![ГДЗ Українська мова 8 клас. Підручник [Глазова О.П.] 2021 ГДЗ Українська мова 8 клас. Підручник [Глазова О.П.] 2021](/uploads/posts/2021-10/1633720388_8k_y_g_2021.jpg)
![ГДЗ Вступ до історії 5 клас. Підручник [Гісем О.В.] 2018 ГДЗ Вступ до історії 5 клас. Підручник [Гісем О.В.] 2018](/uploads/posts/2019-07/1564163269_5k_i_h_2018.jpg)