ГДЗ Геометрія 8 клас. Підручник [Мерзляк А.Г., Полонський В.Б., Якір М.С.] 2021

189. Чи є відрізок MK середньою лінією трикутника ABC (рис. 59)?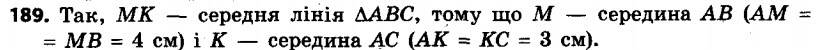
190.° Чи є відрізок EF середньою лінією трикутника MKP (рис. 60)?
191. Відрізки DE і DF — середні лінії трикутника ABC (рис. 61). Чи є відрізок EF середньою лінією цього трикутника?
192. Сторони трикутника дорівнюють 6 см, 8 см і 12 см. Знайдіть середні лінії цього трикутника.
193. Точки M і K — середини сторін AB і AC трикутника ABC відповідно. Знайдіть периметр трикутника ABC, якщо периметр трикутника MAK дорівнює 17 см.
194. Доведіть, що периметр трикутника, сторони якого є середніми лініями трикутника ABC, дорівнює половині периметра трикутника ABC.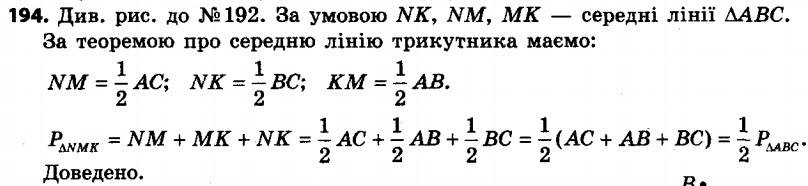
195. Визначте вид трикутника, у якому середні лінії рівні між собою.
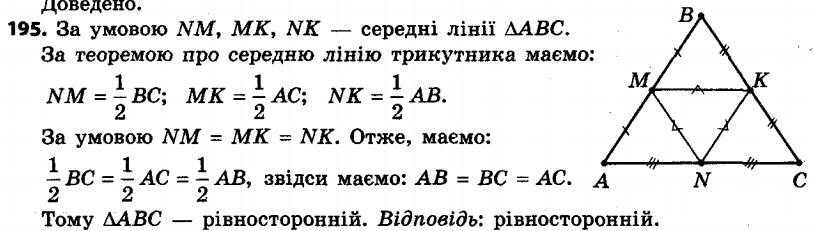196. Доведіть, що середні лінії трикутника розбивають його на чотири рівних трикутники.
197. Точки E і F — відповідно середини сторін AB і BC трикутника ABC. Знайдіть сторону AC, якщо вона на 7 см більша за відрізок EF.
198. Доведіть, що середня лінія DE трикутника ABC (точки D і E належать сторонам AB і BC відповідно) та його медіана BM точкою перетину діляться навпіл.

199. Доведіть, що висота AM трикутника ABC перпендикулярна до його середньої лінії, яка сполучає середини сторін AB і AC.200. Знайдіть кути трикутника, дві середні лінії якого рівні та перпендикулярні.
201. Середня лінія рівнобедреного трикутника, паралельна основі, дорівнює 6 см. Знайдіть сторони даного трикутника, якщо його периметр дорівнює 46 см.
202. Сума діагоналей чотирикутника дорівнює 28 см. Знайдіть периметр чотирикутника, вершини якого є серединами сторін даного чотирикутника.
203. Вершинами чотирикутника є середини сторін ромба з діагоналями 8 см і 14 см. Визначте вид чотирикутника та знайдіть його сторони.
204. Вершинами чотирикутника є середини сторін прямокутника з діагоналлю 12 см. Визначте вид чотирикутника та знайдіть його сторони.
205. Доведіть, що вершини трикутника рівновіддалені від прямої, на якій лежить його середня лінія.
206. На сторонах AB і BC трикутника позначено відповідно точки M і K так, що AM = 3BM, CK = 3BK. Доведіть, що MK || AC, і знайдіть відрізок MK, якщо AC = 16 см
207. Кути BAD і BCE — зовнішні кути трикутника ABC. Із вершини B проведено перпендикуляри BM і BK до бісектрис кутів BAD і BCE відповідно. Знайдіть відрізок MK, якщо периметр трикутника ABC дорівнює 18 см.
208. Побудуйте трикутник за серединами трьох його сторін.
209. Побудуйте паралелограм за серединами трьох його сторін. 210. Діагоналі опуклого чотирикутника ABCD перпендикулярні. Через середини сторін AB і AD проведено прямі, перпендикулярні відповідно до сторін DC і BC. Доведіть, що точка перетину проведених прямих належить прямій AC.
211. Сторони AB і CD опуклого чотирикутника ABCD рівні. Через середини діагоналей AC і BD проведено пряму, яка перетинає сторони AB і CD у точках M і N відповідно. Доведіть, що ∠BMN = ∠CNM.
212. До кола із центром O через точку C проведено дотичні CA і CB (A і B — точки дотику). Відрізок AD — діаметр кола. Доведіть, що BD || CO.
213. У трикутнику ABC відомо, що AB = BC, ∠B = 32°, AK — бісектриса трикутника. Через точку K проведено пряму, яка паралельна стороні AB і перетинає сторону AC у точці M. Знайдіть кут AKM.
214. Діагональ BD паралелограма ABCD є його висотою та дорівнює стороні BC. Знайдіть сторону CD паралелограма, якщо точка B віддалена від прямої CD на 4 см.
215. П’ять точок належать рівносторонньому трикутнику, сторона якого дорівнює 1 см. Доведіть, що із цих точок можна вибрати дві, відстань між якими не більша за 0,5 см.

---

---

Назад

Вперед

1 ... 4 5 6 7 8 9 10 11 12 ... 32

ГДЗ 2021 Підручник 8 клас Геометрія Мерзляк Полонський Якір Гімназія