ГДЗ Геометрія 8 клас. Підручник [Мерзляк А.Г., Полонський В.Б., Якір М.С.] 2021
6. Квадрат
165.° Доведіть, що коли один із кутів ромба прямий, то цей ромб є квадратом. 166. Доведіть, що коли дві сусідні сторони прямокутника рівні, то цей прямокутник є квадратом.
166. Доведіть, що коли дві сусідні сторони прямокутника рівні, то цей прямокутник є квадратом. 167. Діагональ BD квадрата ABCD дорівнює 5 см. Яка довжина діагоналі AC? Чому дорівнюють кути трикутника AOB, де O — точка перетину діагоналей квадрата?
167. Діагональ BD квадрата ABCD дорівнює 5 см. Яка довжина діагоналі AC? Чому дорівнюють кути трикутника AOB, де O — точка перетину діагоналей квадрата? 168. На стороні BC квадрата ABCD (рис. 52) позначили точку K так, що ∠AKB = 74°. Знайдіть кут CAK.
168. На стороні BC квадрата ABCD (рис. 52) позначили точку K так, що ∠AKB = 74°. Знайдіть кут CAK.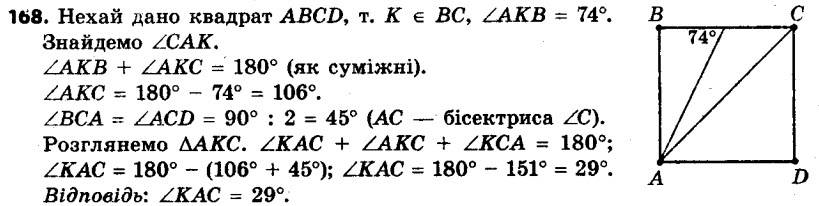 169. На стороні BC квадрата ABCD позначили точку K так, що AK = 2BK. Знайдіть кут KAD.
169. На стороні BC квадрата ABCD позначили точку K так, що AK = 2BK. Знайдіть кут KAD.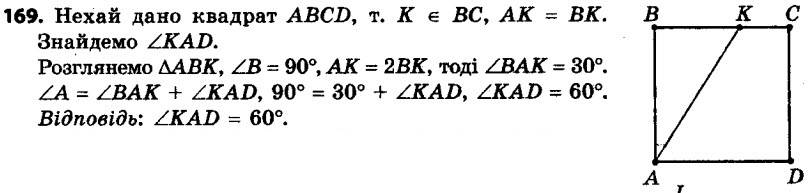 170.° Чи є правильним твердження:
170.° Чи є правильним твердження:1) будь-який квадрат є паралелограмом;
2) будь-який ромб є квадратом;
3) будь-який прямокутник є квадратом;
4) будь-який квадрат є прямокутником;
5) будь-який квадрат є ромбом;
6) якщо діагоналі чотирикутника рівні, то він є прямокутником;
7) якщо діагоналі чотирикутника перпендикулярні, то він є ромбом;
8) існує ромб, який є прямокутником;
9) існує квадрат, який не є ромбом;
10) якщо діагоналі чотирикутника не перпендикулярні, то він не є ромбом;
11) якщо діагоналі паралелограма не рівні, то він не є прямокутником;
12) якщо діагональ прямокутника ділить його кут навпіл, то цей прямокутник є квадратом?
 171. Через вершини квадрата проведено прямі, паралельні його діагоналям. Доведіть, що точки перетину цих прямих є вершинами квадрата.
171. Через вершини квадрата проведено прямі, паралельні його діагоналям. Доведіть, що точки перетину цих прямих є вершинами квадрата. 172. У прямокутному трикутнику через точку перетину бісектриси прямого кута та гіпотенузи проведено прямі, паралельні катетам. Доведіть, що чотирикутник, який утворився, є квадратом.
172. У прямокутному трикутнику через точку перетину бісектриси прямого кута та гіпотенузи проведено прямі, паралельні катетам. Доведіть, що чотирикутник, який утворився, є квадратом.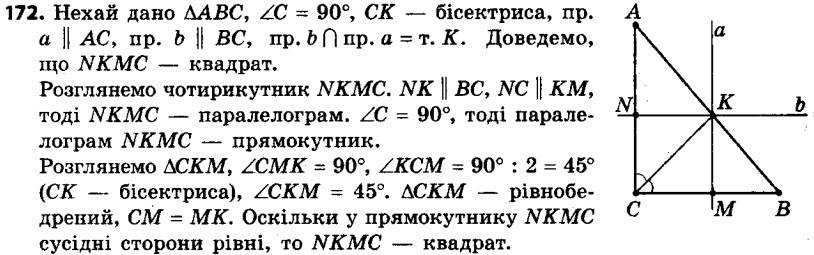 173. Точки M, K, N, P є відповідно серединами сторін AB, BC, CD і AD квадрата ABCD. Доведіть, що чотирикутник MKNP — квадрат.
173. Точки M, K, N, P є відповідно серединами сторін AB, BC, CD і AD квадрата ABCD. Доведіть, що чотирикутник MKNP — квадрат. 174. У трикутнику ABC відомо, що ∠C = 90°, AC = BC = 14 см. Дві сторони квадрата CDEF лежать на катетах трикутника ABC, а вершина E належить гіпотенузі AB. Знайдіть периметр квадрата CDEF.
174. У трикутнику ABC відомо, що ∠C = 90°, AC = BC = 14 см. Дві сторони квадрата CDEF лежать на катетах трикутника ABC, а вершина E належить гіпотенузі AB. Знайдіть периметр квадрата CDEF. 175. У квадраті ABCD позначено точку M так, що трикутник AMB рівносторонній. Доведіть, що трикутник CMD рівнобедрений.
175. У квадраті ABCD позначено точку M так, що трикутник AMB рівносторонній. Доведіть, що трикутник CMD рівнобедрений.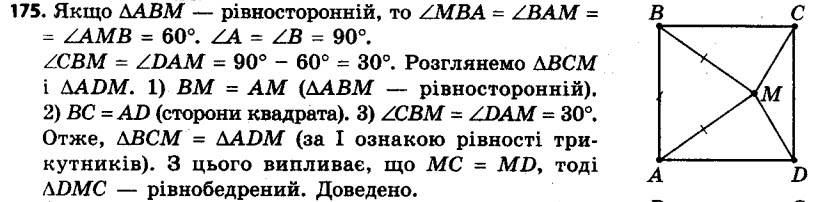 176. Доведіть, що коли діагоналі паралелограма рівні та перпендикулярні, то цей паралелограм є квадратом.
176. Доведіть, що коли діагоналі паралелограма рівні та перпендикулярні, то цей паралелограм є квадратом. 177. Чотирикутники ABCD, DEFM, MNKL, LPOS, SQTV — квадрати (рис. 53). Знайдіть суму довжин тих сторін квадратів, які не лежать на прямій AV, якщо довжина відрізка AV дорівнює 16 см.
177. Чотирикутники ABCD, DEFM, MNKL, LPOS, SQTV — квадрати (рис. 53). Знайдіть суму довжин тих сторін квадратів, які не лежать на прямій AV, якщо довжина відрізка AV дорівнює 16 см. 178. Побудуйте квадрат за його стороною.
178. Побудуйте квадрат за його стороною. 179. Доведіть, що точки перетину бісектрис кутів прямокутника, який не є квадратом, є вершинами квадрата.
179. Доведіть, що точки перетину бісектрис кутів прямокутника, який не є квадратом, є вершинами квадрата.
180. Вершини M і K рівностороннього трикутника AMK належать сторонам BC і CD квадрата ABCD. Доведіть, що MK || BD.
 181. Дано точки M і K. Побудуйте квадрат ABCD так, щоб точка M була серединою сторони AB, а точка K — серединою сторони BC.
181. Дано точки M і K. Побудуйте квадрат ABCD так, щоб точка M була серединою сторони AB, а точка K — серединою сторони BC. 182. Через довільну точку, яка належить квадрату, проведено дві перпендикулярні прямі, кожна з яких перетинає дві протилежні сторони квадрата. Доведіть, що відрізки цих прямих, які належать квадрату, рівні.
182. Через довільну точку, яка належить квадрату, проведено дві перпендикулярні прямі, кожна з яких перетинає дві протилежні сторони квадрата. Доведіть, що відрізки цих прямих, які належать квадрату, рівні. 183. Побудуйте квадрат:
183. Побудуйте квадрат:1) за сумою діагоналі та сторони;
2) за різницею діагоналі та сторони.
 184. У квадраті ABCD позначено точку O так, що ∠OAD = ∠ODA = 15°. Доведіть, що трикутник BOC рівносторонній.
184. У квадраті ABCD позначено точку O так, що ∠OAD = ∠ODA = 15°. Доведіть, що трикутник BOC рівносторонній. 185. На сторонах BC і CD квадрата ABCD позначено точки M і E так, що кути BAM і MAE рівні. Доведіть, що AE = BM + DE.
185. На сторонах BC і CD квадрата ABCD позначено точки M і E так, що кути BAM і MAE рівні. Доведіть, що AE = BM + DE. 186. На рисунку 54 AB || CD, AB = AE, CD = CE. Доведіть, що BE ^ DE.
186. На рисунку 54 AB || CD, AB = AE, CD = CE. Доведіть, що BE ^ DE.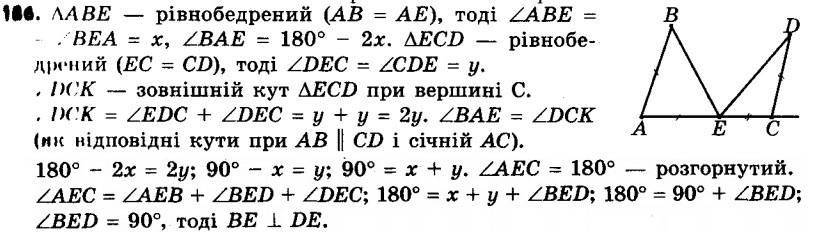 187. На рисунку 55 EF || AD, BF = KF, CF = DF. Доведіть, що EF || BC.
187. На рисунку 55 EF || AD, BF = KF, CF = DF. Доведіть, що EF || BC.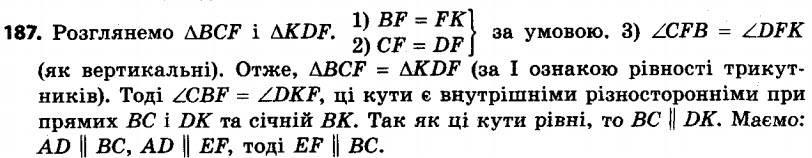
 ГДЗ 2021 Підручник 8 клас Геометрія Мерзляк Полонський Якір Гімназія
ГДЗ 2021 Підручник 8 клас Геометрія Мерзляк Полонський Якір Гімназія
 Якщо помітили в тексті помилку, виділіть її та натисніть Ctrl + Enter
Якщо помітили в тексті помилку, виділіть її та натисніть Ctrl + Enter 15.10.2021,
15.10.2021,
 31 565,
31 565,
 0
0
 Назад
Назад




![ГДЗ Природознавство 5 клас. Підручник [Ярошенко О.Г., Бойко В.М.] 2018 ГДЗ Природознавство 5 клас. Підручник [Ярошенко О.Г., Бойко В.М.] 2018](/uploads/posts/2019-04/1555779316_5_p_y_u2018.jpg)
![ГДЗ Основи правознавства 9 клас. Підручник [Наровлянський О. Д.] 2017 ГДЗ Основи правознавства 9 клас. Підручник [Наровлянський О. Д.] 2017](/uploads/posts/2019-02/1550928122_9k_p_n_2017.jpg)
![ГДЗ Українська мова 8 клас. Підручник [Глазова О.П.] 2021 ГДЗ Українська мова 8 клас. Підручник [Глазова О.П.] 2021](/uploads/posts/2021-10/1633720388_8k_y_g_2021.jpg)
![ГДЗ Вступ до історії 5 клас. Підручник [Гісем О.В.] 2018 ГДЗ Вступ до історії 5 клас. Підручник [Гісем О.В.] 2018](/uploads/posts/2019-07/1564163269_5k_i_h_2018.jpg)