ГДЗ Геометрія 8 клас. Підручник [Мерзляк А.Г., Полонський В.Б., Якір М.С.] 2021
§ 2. Подібність трикутників
11. Теорема Фалеса. Теорема про пропорційні відрізки
368. Накресліть довільний відрізок і поділіть його на п’ять рівних частин. 369. Накресліть довільний відрізок і поділіть його на сім рівних частин.
369. Накресліть довільний відрізок і поділіть його на сім рівних частин. 370. Накресліть довільний відрізок AB і побудуйте на ньому точку C таку, що AC : CB = 2 : 7.
370. Накресліть довільний відрізок AB і побудуйте на ньому точку C таку, що AC : CB = 2 : 7.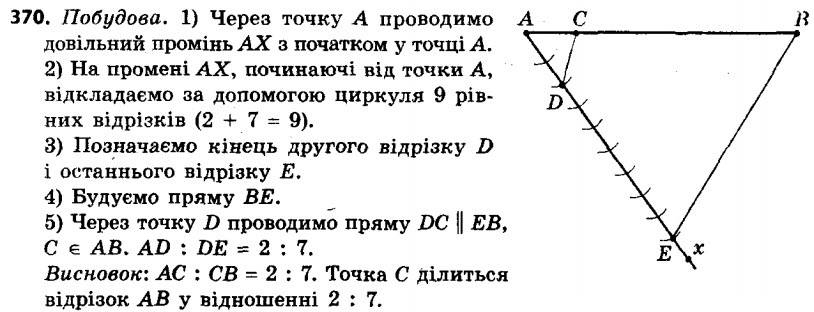
371. Накресліть довільний відрізок CD і побудуйте на ньому точку E таку, що CE : ED = 1 : 5.
 372. На рисунку 121 OA1 = A1A2 = A2A3 = A3A4, A1B1 || A2B2 || A3B3 || A4B4, OB1 = 3 см. Знайдіть відрізки B1B2, OB3, B1B4.
372. На рисунку 121 OA1 = A1A2 = A2A3 = A3A4, A1B1 || A2B2 || A3B3 || A4B4, OB1 = 3 см. Знайдіть відрізки B1B2, OB3, B1B4.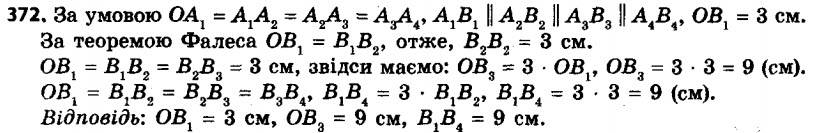 373. На рисунку 122 AB = BC, EF = 5 см. Знайдіть відрізок ED.
373. На рисунку 122 AB = BC, EF = 5 см. Знайдіть відрізок ED. 374. Знайдіть відношення відрізків AB і CD, якщо їхні довжини відповідно дорівнюють 12 см і 18 см. Чи зміниться це відношення, якщо довжини даних відрізків виразити в дециметрах? у міліметрах?
374. Знайдіть відношення відрізків AB і CD, якщо їхні довжини відповідно дорівнюють 12 см і 18 см. Чи зміниться це відношення, якщо довжини даних відрізків виразити в дециметрах? у міліметрах?
375. Чи пропорційні відрізки AB і CD відповідно відрізкам EF і MK, якщо:
1) AB = 16 см, CD = 6 см, EF = 24 см, MK = 9 см;
2) AB = 8 см, CD = 20 см, EF = 10 см, MK = 35 см?
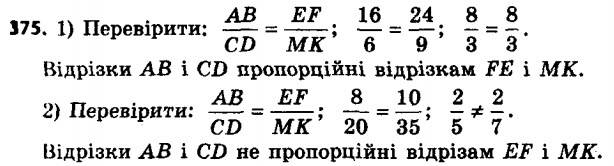 376. Серед відрізків AB, CD, EF, MK, PS виберіть чотири відрізки так, щоб два з них були пропорційними двом іншим відрізкам, якщо AB = 3 см, CD = 16 см, EF = 18 см, MK = 36 см, PS = 6 см.
376. Серед відрізків AB, CD, EF, MK, PS виберіть чотири відрізки так, щоб два з них були пропорційними двом іншим відрізкам, якщо AB = 3 см, CD = 16 см, EF = 18 см, MK = 36 см, PS = 6 см.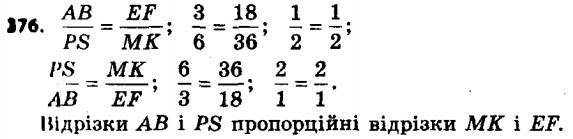 377. На рисунку 123 BD || CE, AB = 16 см, BC = 6 см, AD = 8 см. Знайдіть відрізок DE.
377. На рисунку 123 BD || CE, AB = 16 см, BC = 6 см, AD = 8 см. Знайдіть відрізок DE.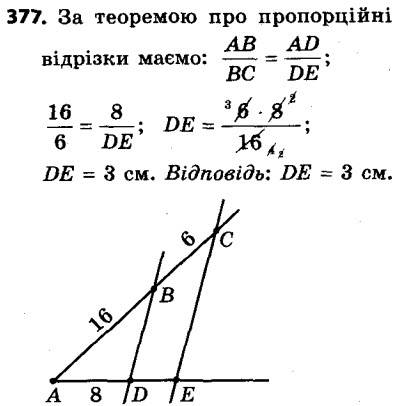
378. На рисунку 124 A1B1 || A2B2 || A3B3, A1A2 = 9 см, A2A3 = 15 см, B1B2 = 6 см. Знайдіть відрізок B2B3.
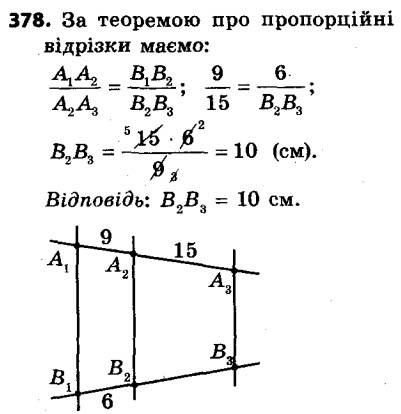 379. На рисунку 125 DE || AC, BE = 10 см, відрізок BD у два рази більший за відрізок AD. Знайдіть відрізок BC.
379. На рисунку 125 DE || AC, BE = 10 см, відрізок BD у два рази більший за відрізок AD. Знайдіть відрізок BC.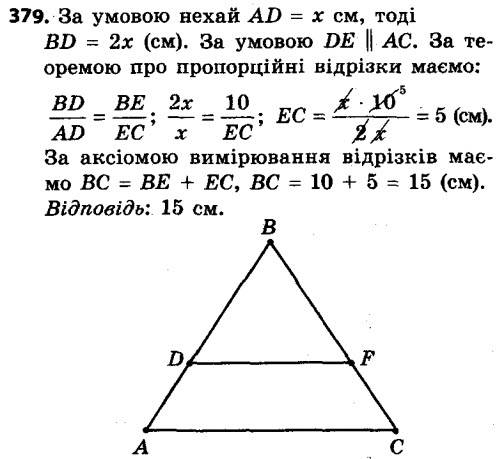 380. Пряма, паралельна стороні BC трикутника ABC, перетинає його сторону AB у точці M, а сторону AC — у точці K, AM = 9 см, BM = 6 см, KC = 8 см. Знайдіть відрізок AK.
380. Пряма, паралельна стороні BC трикутника ABC, перетинає його сторону AB у точці M, а сторону AC — у точці K, AM = 9 см, BM = 6 см, KC = 8 см. Знайдіть відрізок AK.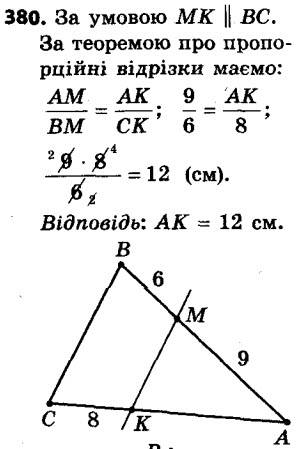 381. Доведіть, що середня лінія трикутника ABC, паралельна стороні AC, ділить навпіл будь-який відрізок, який сполучає вершину B з довільною точкою сторони AC.
381. Доведіть, що середня лінія трикутника ABC, паралельна стороні AC, ділить навпіл будь-який відрізок, який сполучає вершину B з довільною точкою сторони AC. 382. Відстань від точки перетину діагоналей прямокутника до його більшої сторони дорівнює 7 см. Знайдіть довжину меншої сторони прямокутника.
382. Відстань від точки перетину діагоналей прямокутника до його більшої сторони дорівнює 7 см. Знайдіть довжину меншої сторони прямокутника. 383. Висота рівностороннього трикутника дорівнює 12 см. На якій відстані від сторін трикутника розташована точка перетину його бісектрис?
383. Висота рівностороннього трикутника дорівнює 12 см. На якій відстані від сторін трикутника розташована точка перетину його бісектрис?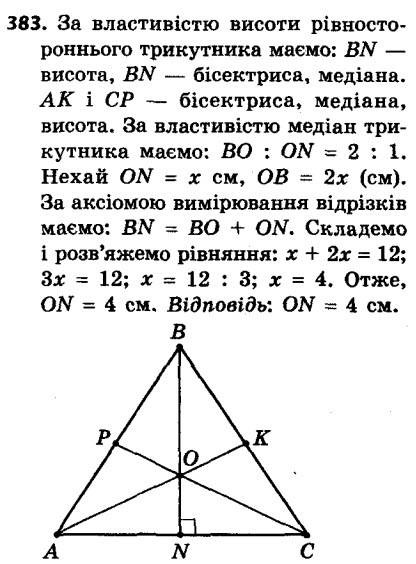 384. Медіана CD трикутника ABC дорівнює 9 см. Знайдіть відрізки CO і OD, де O — точка перетину медіан трикутника ABC.
384. Медіана CD трикутника ABC дорівнює 9 см. Знайдіть відрізки CO і OD, де O — точка перетину медіан трикутника ABC.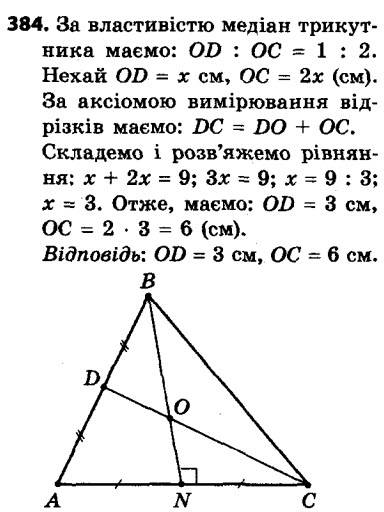 385. Відрізок BD є бісектрисою трикутника ABC, AB = 40 см, AD = 30 см, CD = 12 см. Знайдіть сторону BC.
385. Відрізок BD є бісектрисою трикутника ABC, AB = 40 см, AD = 30 см, CD = 12 см. Знайдіть сторону BC.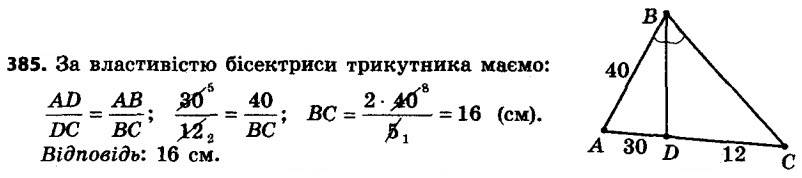 386. Відрізок AM — бісектриса трикутника ABC, AB = 48 см, AC = 32 см, BM = 18 см. Знайдіть сторону BC
386. Відрізок AM — бісектриса трикутника ABC, AB = 48 см, AC = 32 см, BM = 18 см. Знайдіть сторону BC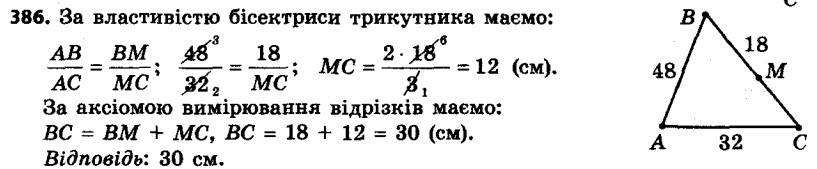 387. Кінці відрізка, який не перетинає дану пряму, віддалені від цієї прямої на 8 см і 14 см. Знайдіть відстань від середини цього відрізка до даної прямої.
387. Кінці відрізка, який не перетинає дану пряму, віддалені від цієї прямої на 8 см і 14 см. Знайдіть відстань від середини цього відрізка до даної прямої. 388. Відстань від середини хорди BC до діаметра AC дорівнює 3 см, ∠BAC = 30°. Знайдіть хорду AB.
388. Відстань від середини хорди BC до діаметра AC дорівнює 3 см, ∠BAC = 30°. Знайдіть хорду AB. 389. Відрізок BM — висота ромба ABCD, проведена до сторони AD, ∠A = 45°, AM = 8 см. Знайдіть відстань від точки перетину діагоналей ромба до сторони AD.
389. Відрізок BM — висота ромба ABCD, проведена до сторони AD, ∠A = 45°, AM = 8 см. Знайдіть відстань від точки перетину діагоналей ромба до сторони AD. 390. У трикутнику ABC відомо, що AB = BC, AC = 8 см, AD — медіана, BE — висота, BE = 12 см. Із точки D опущено перпендикуляр DF на сторону AC. Знайдіть відрізок DF і кут ADF.
390. У трикутнику ABC відомо, що AB = BC, AC = 8 см, AD — медіана, BE — висота, BE = 12 см. Із точки D опущено перпендикуляр DF на сторону AC. Знайдіть відрізок DF і кут ADF. 391. Сторона AC трикутника ABC дорівнює 24 см. Сторону AB поділили на чотири рівних відрізки та через точки поділу провели прямі, паралельні стороні AC. Знайдіть відрізки цих прямих, які належать трикутнику.
391. Сторона AC трикутника ABC дорівнює 24 см. Сторону AB поділили на чотири рівних відрізки та через точки поділу провели прямі, паралельні стороні AC. Знайдіть відрізки цих прямих, які належать трикутнику. 392. Основи трапеції дорівнюють 16 см і 28 см. Одну з бічних сторін поділили на три рівних відрізки та через точки поділу провели прямі, паралельні основам. Знайдіть відрізки цих прямих, які належать трапеції.
392. Основи трапеції дорівнюють 16 см і 28 см. Одну з бічних сторін поділили на три рівних відрізки та через точки поділу провели прямі, паралельні основам. Знайдіть відрізки цих прямих, які належать трапеції. 393. Сторону DE трикутника DEF поділили на три рівних відрізки та через точки поділу провели прямі, паралельні стороні DF. Знайдіть відрізки цих прямих, які належать трикутнику DEF, якщо DF = 15 см
393. Сторону DE трикутника DEF поділили на три рівних відрізки та через точки поділу провели прямі, паралельні стороні DF. Знайдіть відрізки цих прямих, які належать трикутнику DEF, якщо DF = 15 см 394. Доведіть, що середня лінія трапеції ділить її діагоналі навпіл.
394. Доведіть, що середня лінія трапеції ділить її діагоналі навпіл. 395. Середня лінія MK трапеції ABCD перетинає діагональ AC у точці E, ME = 4 см, EK = 6 см. Знайдіть основи трапеції.
395. Середня лінія MK трапеції ABCD перетинає діагональ AC у точці E, ME = 4 см, EK = 6 см. Знайдіть основи трапеції. 396. Діагоналі трапеції перетинають її середню лінію MK у точках E і F. Доведіть, що ME = KF.
396. Діагоналі трапеції перетинають її середню лінію MK у точках E і F. Доведіть, що ME = KF. 397. Основи трапеції дорівнюють 12 см і 22 см. Знайдіть відрізки, на які діагоналі трапеції ділять її середню лінію.
397. Основи трапеції дорівнюють 12 см і 22 см. Знайдіть відрізки, на які діагоналі трапеції ділять її середню лінію. 398. На рисунку 126 AE || BF || CM || DK, AB = 25 см, BC = 20 см, CD = 35 см, EK = 48 см. Знайдіть відрізки EF, FM і MK.
398. На рисунку 126 AE || BF || CM || DK, AB = 25 см, BC = 20 см, CD = 35 см, EK = 48 см. Знайдіть відрізки EF, FM і MK. 399. Через точку D, позначену на стороні AC трикутника ABC, проведено пряму, яка паралельна стороні AB і перетинає сторону BC у точці E. Знайдіть відрізок BE, якщо AD : DC = 5 : 7, BC = 36 см.
399. Через точку D, позначену на стороні AC трикутника ABC, проведено пряму, яка паралельна стороні AB і перетинає сторону BC у точці E. Знайдіть відрізок BE, якщо AD : DC = 5 : 7, BC = 36 см. 400. Точки M і K — середини сторін AB і AD паралелограма ABCD відповідно. Доведіть, що точка перетину прямих BK і DM належить діагоналі AC.
400. Точки M і K — середини сторін AB і AD паралелограма ABCD відповідно. Доведіть, що точка перетину прямих BK і DM належить діагоналі AC. 401. Доведіть, що коли дві медіани трикутника рівні, то цей трикутник рівнобедрений.
401. Доведіть, що коли дві медіани трикутника рівні, то цей трикутник рівнобедрений. 402. У трикутнику ABC (AB = BC) проведено медіану AM і висоту BH. Знайдіть висоту BH, якщо AM = 45 см, ∠CAM = 30°.
402. У трикутнику ABC (AB = BC) проведено медіану AM і висоту BH. Знайдіть висоту BH, якщо AM = 45 см, ∠CAM = 30°. 403. Дано відрізок AB і точку O, яка не належить прямій AB. Побудуйте трикутник, для якого відрізок AB є стороною, а точка O — точкою перетину медіан.
403. Дано відрізок AB і точку O, яка не належить прямій AB. Побудуйте трикутник, для якого відрізок AB є стороною, а точка O — точкою перетину медіан. 404. Відрізок BD — бісектриса трикутника ABC, AB = 28 см, BC = 20 см, AC = 36 см. Знайдіть відрізки AD і CD.
404. Відрізок BD — бісектриса трикутника ABC, AB = 28 см, BC = 20 см, AC = 36 см. Знайдіть відрізки AD і CD.
405. У трикутник ABC вписано ромб CDEF так, що кут C у них спільний, а вершини D, E і F ромба належать відповідно сторонам AC, AB і BC трикутника. Знайдіть сторони AC і BC, якщо AE = 30 см, BE = 12 см, а периметр трикутника дорівнює 105 см.
 406. Сторони трикутника дорівнюють 39 см, 65 см і 80 см. Коло, центр якого належить більшій стороні трикутника, дотикається до двох інших його сторін. На які відрізки центр цього кола ділить сторону трикутника?
406. Сторони трикутника дорівнюють 39 см, 65 см і 80 см. Коло, центр якого належить більшій стороні трикутника, дотикається до двох інших його сторін. На які відрізки центр цього кола ділить сторону трикутника? 407. Точка D — середина основи AC рівнобедреного трикутника ABC. На стороні AB позначили точку M так, що AM : MB = 2 : 7. У якому відношенні пряма BD ділить відрізок CM?
407. Точка D — середина основи AC рівнобедреного трикутника ABC. На стороні AB позначили точку M так, що AM : MB = 2 : 7. У якому відношенні пряма BD ділить відрізок CM? 408. У рівнобедреному трикутнику DEF провели висоту EC до його основи та на бічній стороні EF позначили точку A. Відрізки EC і DA перетинаються в точці O, причому AO : OD = 3 : 8. Знайдіть відношення EA : AF.
408. У рівнобедреному трикутнику DEF провели висоту EC до його основи та на бічній стороні EF позначили точку A. Відрізки EC і DA перетинаються в точці O, причому AO : OD = 3 : 8. Знайдіть відношення EA : AF. 409. У рівнобедреному трикутнику висота, проведена до основи, дорівнює 42 см, а основа відноситься до бічної сторони як 6 : 11. Знайдіть радіус кола, вписаного в даний трикутник.
409. У рівнобедреному трикутнику висота, проведена до основи, дорівнює 42 см, а основа відноситься до бічної сторони як 6 : 11. Знайдіть радіус кола, вписаного в даний трикутник. 410. Бічна сторона рівнобедреного трикутника дорівнює 60 см, а центр вписаного кола ділить медіану, проведену до основи, у відношенні 12 : 5. Знайдіть основу трикутника.
410. Бічна сторона рівнобедреного трикутника дорівнює 60 см, а центр вписаного кола ділить медіану, проведену до основи, у відношенні 12 : 5. Знайдіть основу трикутника. 411. На стороні BC трикутника ABC позначено точку M так, що BM : MC = 3 : 10. У якому відношенні відрізок AM ділить медіану BK трикутника ABC?
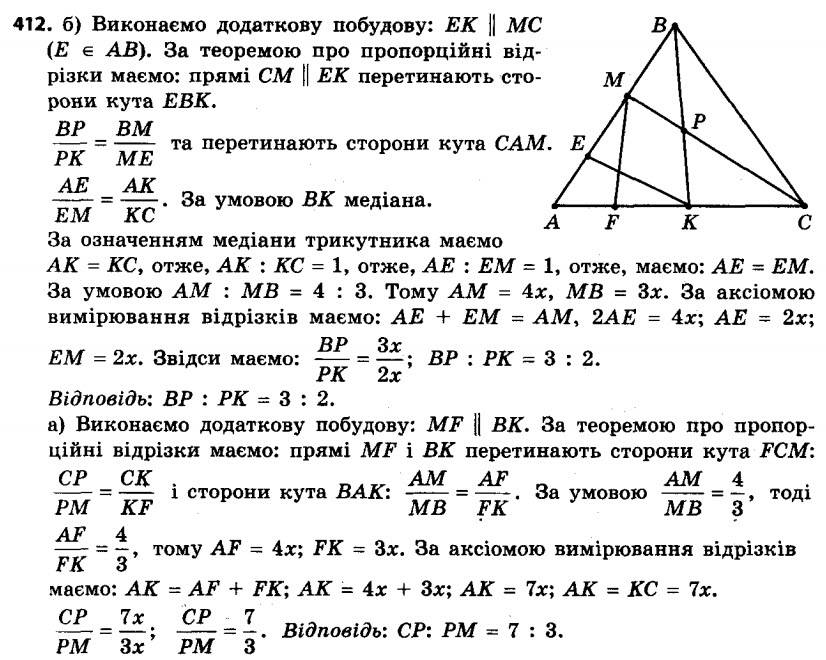
411. На стороні BC трикутника ABC позначено точку M так, що BM : MC = 3 : 10. У якому відношенні відрізок AM ділить медіану BK трикутника ABC?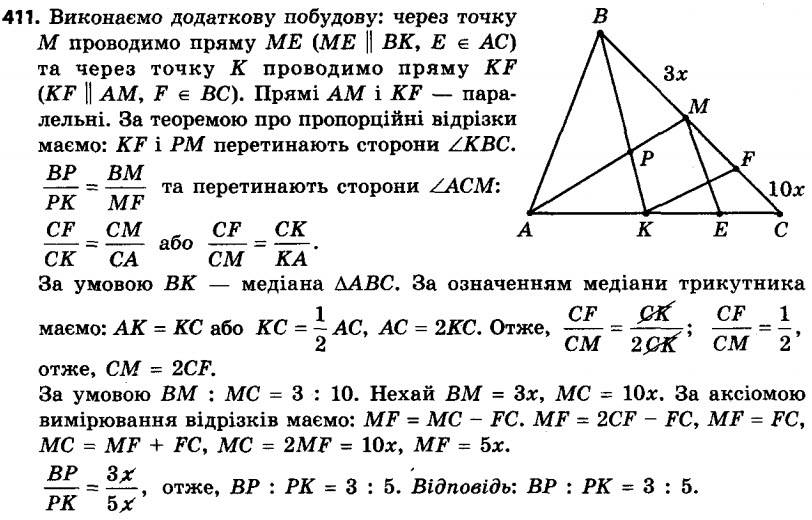 412. На стороні AB трикутника ABC позначено точку M так, що AM : MB = 4 : 3. У якому відношенні медіана BK:
412. На стороні AB трикутника ABC позначено точку M так, що AM : MB = 4 : 3. У якому відношенні медіана BK:1) ділить відрізок CM;
2) ділиться відрізком CM?
 413. Доведіть, що відрізок, який сполучає середини діагоналей трапеції, паралельний її основам і дорівнює половині їхньої різниці.
413. Доведіть, що відрізок, який сполучає середини діагоналей трапеції, паралельний її основам і дорівнює половині їхньої різниці. 414. Дано відрізки a, b, c. Побудуйте відрізок x такий, що a : x = = b : c.
414. Дано відрізки a, b, c. Побудуйте відрізок x такий, що a : x = = b : c. 415. Через точку O, яка належить даному куту, проведіть відрізок, кінці якого належать сторонам даного кута та який ділиться точкою O:
415. Через точку O, яка належить даному куту, проведіть відрізок, кінці якого належать сторонам даного кута та який ділиться точкою O:1) навпіл;
2) у відношенні 2 : 3.
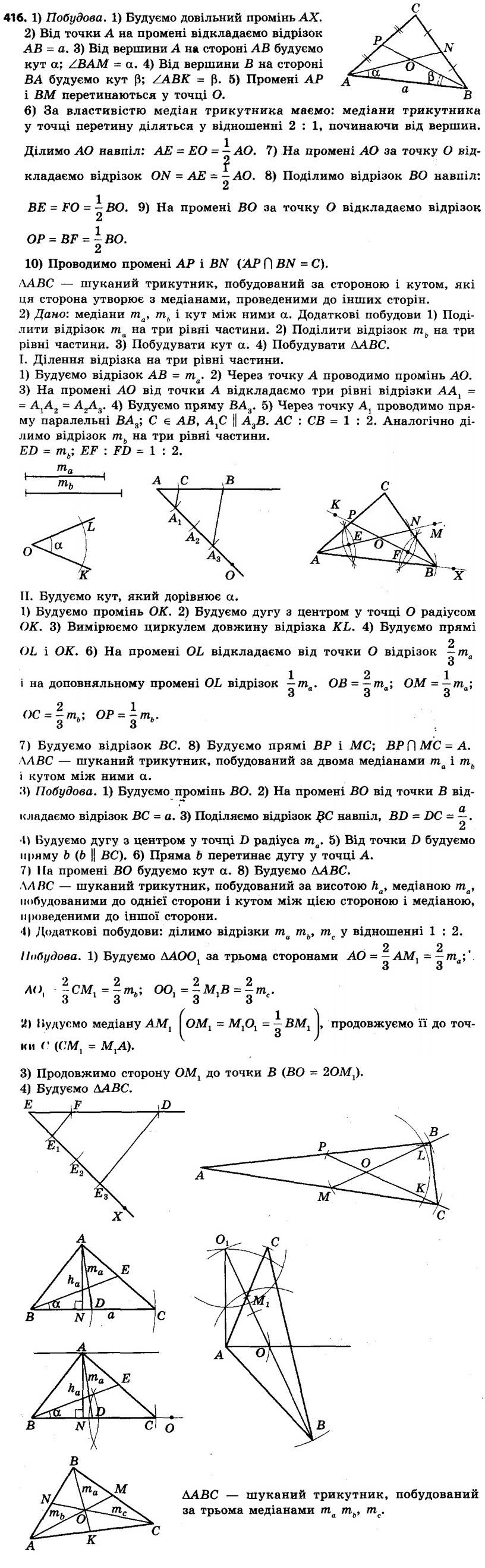
 416. Побудуйте трикутник:
416. Побудуйте трикутник:1) за стороною та кутами, які ця сторона утворює з медіанами, проведеними до двох інших сторін;
2) за двома медіанами та кутом між ними;
3) за висотою та медіаною, проведеними до однієї сторони, і кутом між цією стороною та медіаною, проведеною до іншої сторони;
4) за трьома медіанами.
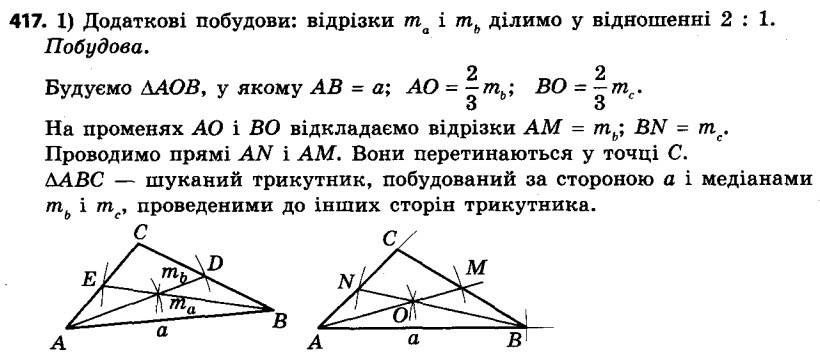
417. Побудуйте трикутник:
1) за стороною та медіанами, проведеними до двох інших сторін;
2) за висотою, проведеною до однієї зі сторін, і медіанами, проведеними до двох інших сторін.
418.•• На сторонах кута A позначено точки B1, B2, C1, C2 так, що AB1/B1B2 = AC1/C1C2 = (рис. 127). Доведіть, що B1C1 || B2C2.
 419. Бісектриса зовнішнього кута при вершині B трикутника ABC перетинає промінь AC у точці D. Доведіть, що AB : BC = AD : CD.
419. Бісектриса зовнішнього кута при вершині B трикутника ABC перетинає промінь AC у точці D. Доведіть, що AB : BC = AD : CD. 420. Сторона квадрата ABCD дорівнює a. На дузі AC кола із центром B, радіус якого дорівнює a, позначено точку E таку, що ∠BEC = 75°. Знайдіть відрізок AE.
420. Сторона квадрата ABCD дорівнює a. На дузі AC кола із центром B, радіус якого дорівнює a, позначено точку E таку, що ∠BEC = 75°. Знайдіть відрізок AE. 421. Діагональ трапеції перпендикулярна до її основ, тупий кут, прилеглий до більшої основи, дорівнює 120°, бічна сторона, прилегла до цього кута, — 12 см, а більша основа — 16 см. Знайдіть середню лінію трапеції.
421. Діагональ трапеції перпендикулярна до її основ, тупий кут, прилеглий до більшої основи, дорівнює 120°, бічна сторона, прилегла до цього кута, — 12 см, а більша основа — 16 см. Знайдіть середню лінію трапеції. 422. Рівносторонній трикутник покрито п’ятьма меншими рівними між собою рівносторонніми трикутниками. Доведіть, що для покриття досить і чотирьох таких трикутників.
422. Рівносторонній трикутник покрито п’ятьма меншими рівними між собою рівносторонніми трикутниками. Доведіть, що для покриття досить і чотирьох таких трикутників.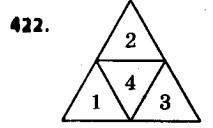
 ГДЗ 2021 Підручник 8 клас Геометрія Мерзляк Полонський Якір Гімназія
ГДЗ 2021 Підручник 8 клас Геометрія Мерзляк Полонський Якір Гімназія
 Якщо помітили в тексті помилку, виділіть її та натисніть Ctrl + Enter
Якщо помітили в тексті помилку, виділіть її та натисніть Ctrl + Enter 15.10.2021,
15.10.2021,
 31 565,
31 565,
 0
0
 Назад
Назад




![ГДЗ Природознавство 5 клас. Підручник [Ярошенко О.Г., Бойко В.М.] 2018 ГДЗ Природознавство 5 клас. Підручник [Ярошенко О.Г., Бойко В.М.] 2018](/uploads/posts/2019-04/1555779316_5_p_y_u2018.jpg)
![ГДЗ Основи правознавства 9 клас. Підручник [Наровлянський О. Д.] 2017 ГДЗ Основи правознавства 9 клас. Підручник [Наровлянський О. Д.] 2017](/uploads/posts/2019-02/1550928122_9k_p_n_2017.jpg)
![ГДЗ Українська мова 8 клас. Підручник [Глазова О.П.] 2021 ГДЗ Українська мова 8 клас. Підручник [Глазова О.П.] 2021](/uploads/posts/2021-10/1633720388_8k_y_g_2021.jpg)
![ГДЗ Вступ до історії 5 клас. Підручник [Гісем О.В.] 2018 ГДЗ Вступ до історії 5 клас. Підручник [Гісем О.В.] 2018](/uploads/posts/2019-07/1564163269_5k_i_h_2018.jpg)