ГДЗ Геометрія 8 клас. Підручник [Мерзляк А.Г., Полонський В.Б., Якір М.С.] 2021

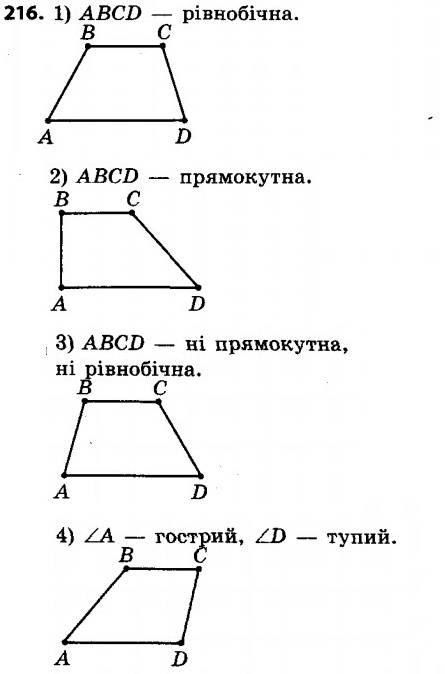
216. Накресліть, використовуючи клітинки зошита, трапецію:
1) рівнобічну;
2) прямокутну;
3) яка не є ні прямокутною, ні рівнобічною;
4) у якої один із кутів при основі гострий, а другий кут при цій самій основі тупий.
217. Перерисуйте в зошит рисунок 72, проведіть висоти трапеції, одним із кінців яких є відповідно точки B, M, K і D.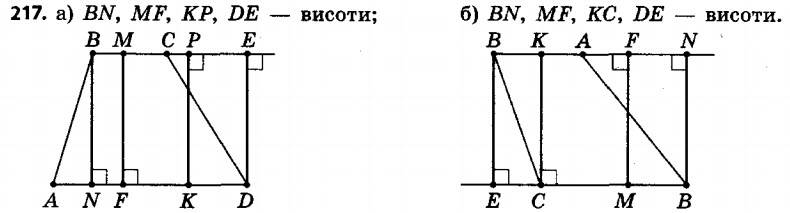
218. Знайдіть на рисунку 73 трапеції, укажіть їхні основи та бічні сторони.
219. Чи є чотирикутник ABCD, зображений на рисунку 74, трапецією? У разі ствердної відповіді вкажіть основи та бічні сторони трапеції.
220. Периметр рівнобічної трапеції дорівнює 52 см, основи — 13 см і 21 см. Знайдіть бічну сторону трапеції.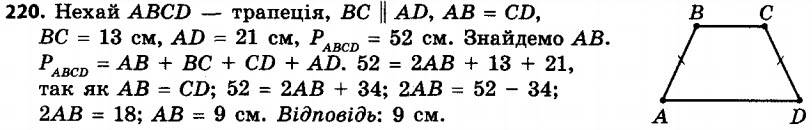
221. Периметр трапеції дорівнює 49 см, бічні сторони — 5,6 см і 7,8 см. Знайдіть основи трапеції, якщо одна з них на 7,4 см більша за другу.
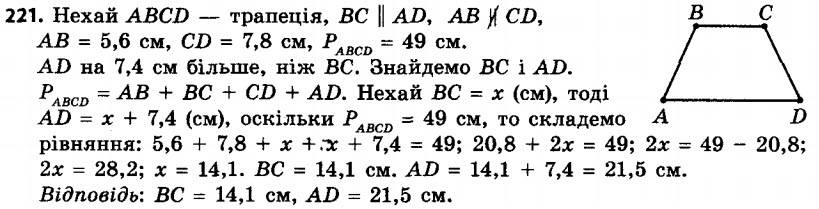222. Доведіть, що сума кутів трапеції, прилеглих до її бічної сторони, дорівнює 180°.
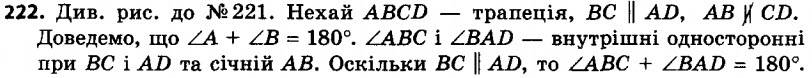223.
1) Знайдіть кути A і C трапеції ABCD з основами AD і BC, якщо ∠B = 132°, ∠D = 24°.
2) Знайдіть кути трапеції ABCD, прилеглі до бічної сторони AB, якщо кут A менший від кута B на 38°.
224. Знайдіть кути трапеції ABCD, прилеглі до бічної сторони CD, якщо ∠C : ∠D = 8 : 7.
225. Один із кутів рівнобічної трапеції дорівнює 46°. Знайдіть решту її кутів.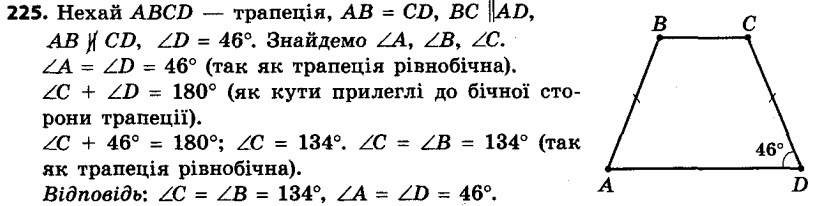
226. Знайдіть кути рівнобічної трапеції, якщо різниця її протилежних кутів дорівнює 20°.
227. У рівнобічній трапеції кут між бічною стороною та висотою, проведеною з вершини тупого кута, дорівнює 23°. Знайдіть кути трапеції.
228.° Чи можуть у трапеції бути:
1) три прямих кути;
2) три гострих кути;
3) два протилежних кути тупими;
4) два протилежних кути прямими;
5) два протилежних кути рівними?
1) Ні;
2) Ні;
3) Ні;
4) Ні;
5) Ні;
229. Чи можуть:
1) основи трапеції бути рівними;
2) діагоналі трапеції точкою перетину ділитися навпіл?
230. Доведіть, що коли кути при одній з основ трапеції рівні, то дана трапеція є рівнобічною.
231. Доведіть, що сума протилежних кутів рівнобічної трапеції дорівнює 180°. Чи є правильним обернене твердження: якщо сума протилежних кутів трапеції дорівнює 180°, то дана трапеція є рівнобічною?
232. Середня лінія рівностороннього трикутника зі стороною 6 см розбиває його на трикутник і чотирикутник. Визначте вид чотирикутника та знайдіть його периметр.
233. Висота рівнобічної трапеції, проведена з кінця меншої основи, ділить більшу основу на відрізки завдовжки 6 см і 10 см. Знайдіть основи трапеції.
234. Один із кутів рівнобічної трапеції дорівнює 60°, бічна сторона — 18 см, а сума основ — 50 см. Знайдіть основи трапеції.
235. Основи прямокутної трапеції дорівнюють 10 см і 24 см, а один із кутів — 45°. Знайдіть меншу бічну сторону трапеції.
236. Основи прямокутної трапеції дорівнюють 7 см і 15 см, а один із кутів — 60°. Знайдіть більшу бічну сторону трапеції.
237. У трапеції ABCD відомо, що AB = CD, ∠BAC = 20°, ∠CAD = 50°. Знайдіть кути ACB і ACD.
238. У трапеції ABCD відомо, що BC || AD, AB ^ AD, BC = CD, ∠ABD = 80°. Знайдіть кути трапеції.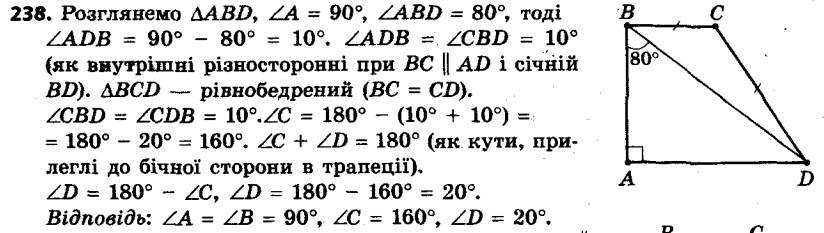
239. У трапеції ABCD менша основа BC дорівнює 6 см. Через вершину B проведено пряму, яка паралельна стороні CD і перетинає сторону AD у точці M. Знайдіть периметр трапеції, якщо периметр трикутника ABM дорівнює 16 см.
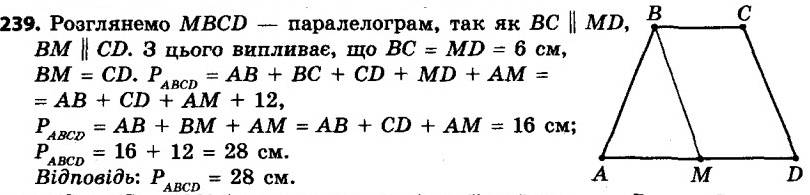240. Через вершину C трапеції ABCD проведено пряму, яка паралельна бічній стороні AB і перетинає більшу основу AD у точці E. Знайдіть кути трапеції, якщо ∠D = 35°, ∠DCE = 65°.
241. Основи трапеції дорівнюють 9 см і 15 см. Чому дорівнює її середня лінія?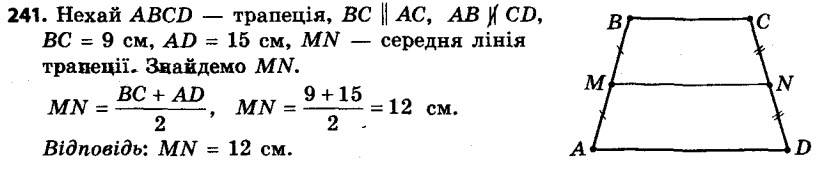
242. Середня лінія трапеції дорівнює 8 см, а одна з основ — 5 см. Знайдіть другу основу трапеції.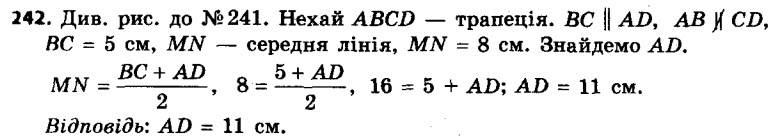

243. Одна з основ трапеції на 8 см більша за другу, а середня лінія дорівнює 17 см. Знайдіть основи трапеції.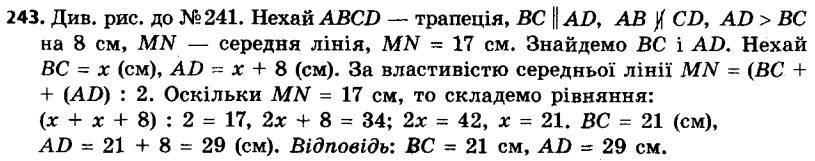244. Основи трапеції відносяться як 3 : 4, а середня лінія дорівнює 14 см. Знайдіть основи трапеції.
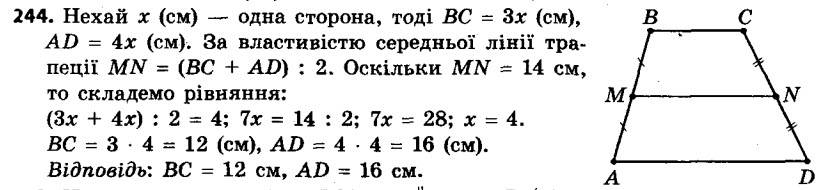245. Кожну з бічних сторін трапеції ABCD (рис. 75) поділено на чотири рівні частини: AE = EF = FK = KB, DN = NM = = MP = PC. Знайдіть відрізки EN, FM і KP, якщо AD = 19 см, BC = 11 см.
246. Висота прямокутної трапеції, проведена з вершини тупого кута, ділить більшу основу на відрізки завдовжки 7 см і 5 см, рахуючи від вершини прямого кута. Знайдіть середню лінію трапеції.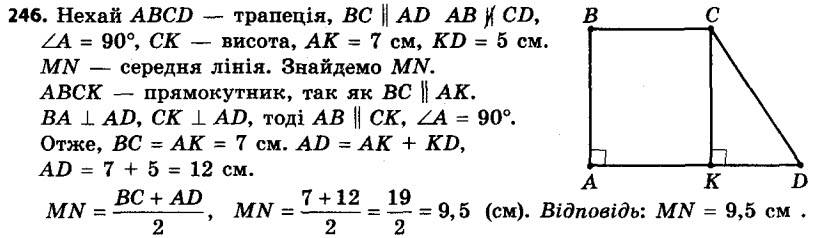
247. Середня лінія прямокутної трапеції дорівнює 9 см, а висота, проведена з вершини тупого кута, ділить більшу основу на відрізки, один з яких у 2 рази більший за другий, рахуючи від вершини прямого кута. Знайдіть основи трапеції.
248. Діагоналі рівнобічної трапеції ABCD (AB = CD) перетинаються в точці O. Доведіть, що AO = OD і BO = OC.
249. Висота рівнобічної трапеції дорівнює h, а бічну сторону видно з точки перетину діагоналей під кутом1 60°. Знайдіть діагональ трапеції.
250. Основи рівнобічної трапеції відносяться як 2 : 5, а діагональ ділить тупий кут трапеції навпіл. Знайдіть сторони трапеції, якщо її периметр дорівнює 68 см.
251. У трапеції ABCD відомо, що AB = CD, AD = 24 см, ∠ADB = = ∠CDB, а периметр дорівнює 60 см. Знайдіть невідомі сторони трапеції.
252. Сторони трапеції дорівнюють a, a, a і 2a. Знайдіть кути трапеції.
253. У трапеції ABCD діагональ AC перпендикулярна до бічної сторони CD і є бісектрисою кута BAD, ∠D = 60°, периметр трапеції дорівнює 40 см. Знайдіть основи трапеції.
254. Діагональ рівнобічної трапеції перпендикулярна до бічної сторони, а менша основа дорівнює бічній стороні. Знайдіть кути трапеції.
255. За якої умови висота рівнобічної трапеції дорівнює половині різниці основ?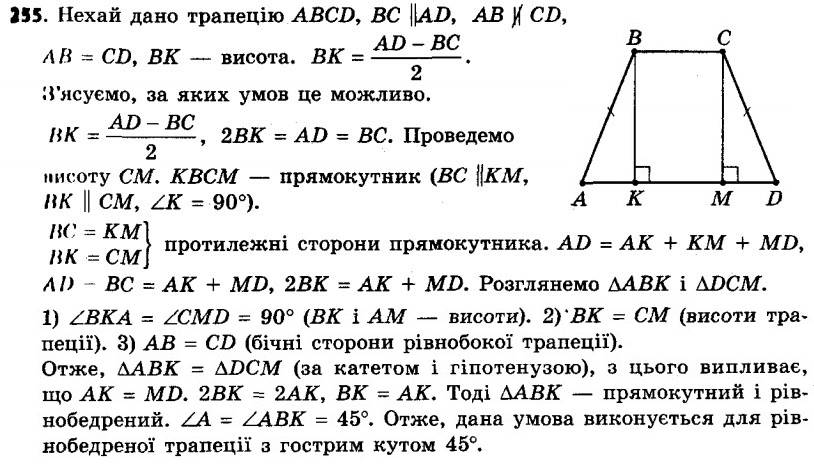
256. Побудуйте рівнобічну трапецію за основою, бічною стороною та кутом між ними.
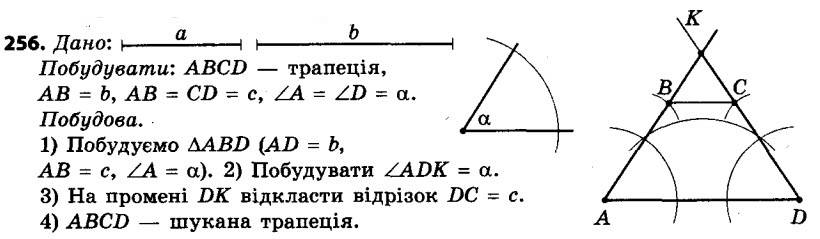257. Побудуйте прямокутну трапецію за основами та меншою бічною стороною.
258. Побудуйте рівнобічну трапецію за основою, бічною стороною та діагоналлю.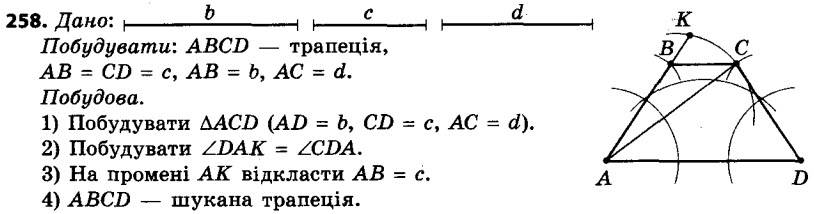
259. Бічна сторона рівнобічної трапеції дорівнює 6 см, більша основа — 10 см. Знайдіть середню лінію трапеції, якщо один з її кутів дорівнює 60°.
260. Діагональ рівнобічної трапеції дорівнює 14 см і утворює з основою кут 60°. Знайдіть середню лінію трапеції.
261. Середня лінія трапеції ABCD розбиває її на дві трапеції, середні лінії яких дорівнюють 15 см і 19 см. Знайдіть основи трапеції ABCD.
262. Доведіть, що коли діагоналі рівнобічної трапеції перпендикулярні, то її висота дорівнює середній лінії трапеції.
263. Доведіть, що коли висота рівнобічної трапеції дорівнює її середній лінії, то діагоналі трапеції перпендикулярні.
264. Діагональ прямокутної трапеції розбиває її на два трикутники, один з яких є рівностороннім зі стороною a. Знайдіть середню лінію трапеції.
265. Діагональ рівнобічної трапеції розбиває її на два рівнобедрених трикутники. Знайдіть кути трапеції.

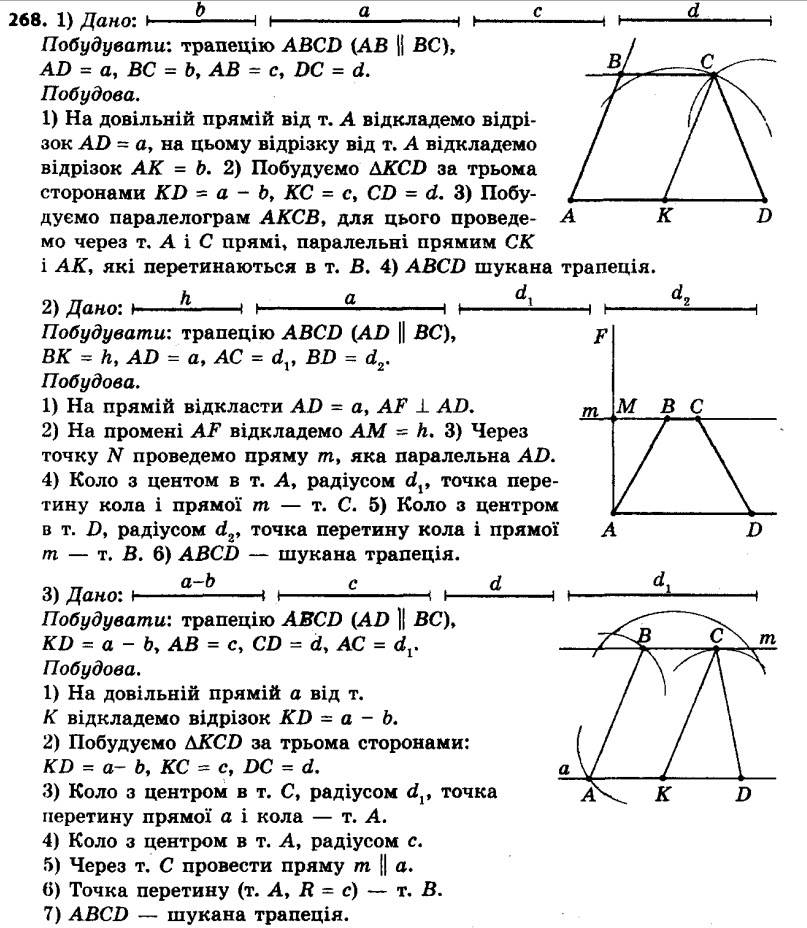
266. У трапеції ABCD (BC || AD) відомо, що AC ^ BD, ∠CAD = 30°, BD = 8 см. Знайдіть середню лінію трапеції.267. Доведіть, що точка перетину бісектрис кутів, прилеглих до бічної сторони трапеції, належить прямій, яка містить її середню лінію.
268. Побудуйте трапецію:
1) за основами та бічними сторонами;
2) за основою, висотою та діагоналями;
3) за різницею основ, бічними сторонами та діагоналлю.
269. Побудуйте рівнобічну трапецію за основою, висотою та бічною стороною.
270. Побудуйте трапецію:
1) за основами та діагоналями;
2) за бічними сторонами, середньою лінією та висотою;
3) за основою, прилеглим до неї кутом і бічними сторонами;
4) за бічними сторонами, висотою та однією з діагоналей.
271. Через вершину B паралелограма ABCD проведено пряму, яка не має з паралелограмом інших спільних точок. Вершини A і C віддалені від цієї прямої на відстані a і b відповідно. Знайдіть відстань від точки D до цієї прямої.
272. У колі проведено діаметри AB і CD. Доведіть, що AC = BD і AC || BD.

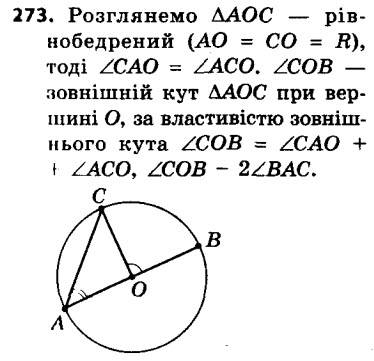
273. У колі з центром O проведено діаметр AB і хорду AC. Доведіть, що ∠BOC = 2 ∠BAC.
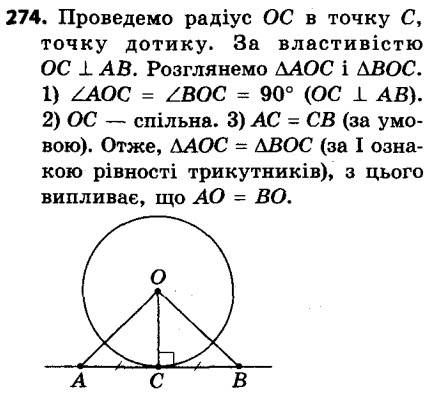
274. Пряма AB дотикається до кола з центром O в точці C, AC = BC. Доведіть, що OA = OB.275. Хорда AB кола з центром O перпендикулярна до радіуса OC і ділить його навпіл. Знайдіть: 1) кут AOB; 2) кут ACB.
276. Скільки спільних точок мають два кола з радіусами 6 см і 8 см, якщо відстань між їхніми центрами дорівнює: 1) 15 см; 2) 14 см; 3) 10 см; 4) 2 см?

---

---

Назад

Вперед

1 ... 5 6 7 8 9 10 11 12 13 ... 32

ГДЗ 2021 Підручник 8 клас Геометрія Мерзляк Полонський Якір Гімназія