ГДЗ Геометрія 8 клас. Підручник [Мерзляк А.Г., Полонський В.Б., Якір М.С.] 2021

15.10.2021, icon

8 Клас / Геометрія, icon

21 852,

Інші завдання дивись тут...

12. Подібні трикутники

423. На рисунку 134 зображено подібні трикутники ABC і DEF, рівні кути яких позначено однаковою кількістю дужок. Які сторони цих трикутників пропорційні? Запишіть відповідні рівності.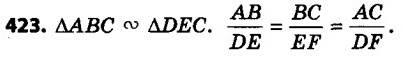

424. Чи подібні трикутники ABC і MNK, якщо ∠A = 40°, ∠B = 82°, ∠M = 40°, ∠K = 58°, AB = 2,4 см, BC = 2,1 см, AC = 3,9 см, MN = 3,2 см, NK = 2,8 см, MK = 5,2 см?

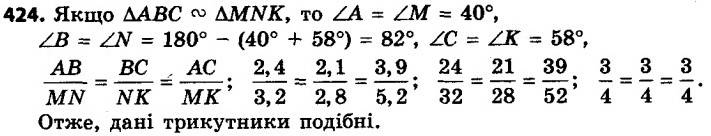425. Відомо, що DDEF 0 3, " DMCP, причому стороні DE відповідає сторона MC, стороні DF — сторона MP, MC = 12 см, MP = = 8 см, EF = 4,5 см. Знайдіть невідомі сторони даних трикутників.

426. Відомо, що DABC " DA1B1C1, причому ∠A = ∠A1, ∠B = ∠B1, AB = 6 см, BC = 7 см, AC = 10 см, A1B1 = 9 см. Знайдіть сторони B1C1 і A1C1.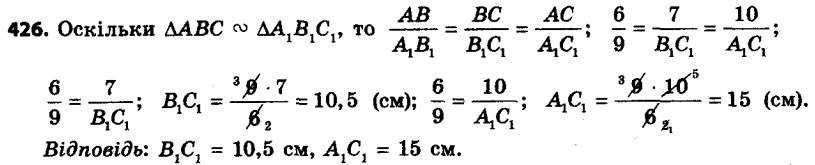

427. Знайдіть кути трикутника A1B1C1, якщо DABC " DA1B1C1, причому стороні AB відповідає сторона A1B1, стороні BC — сторона B1C1, ∠A = 25°, ∠B = 70°.

428. Сторони MK і DE, KT і EF — відповідні сторони подібних трикутників MKT і DEF, MK = 18 см, KT = 16 см, MT = 28 см, MK : DE = 4 : 5. Знайдіть сторони трикутника DEF.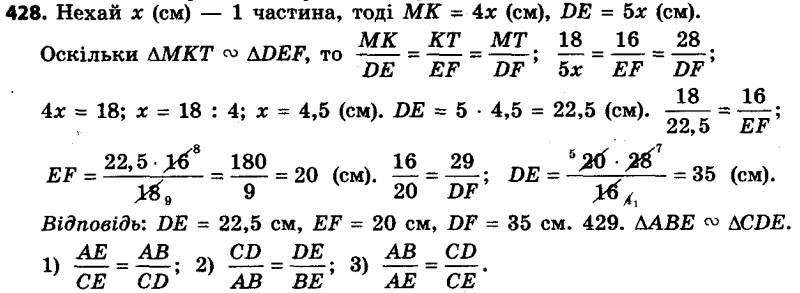

430. Пряма, паралельна стороні AC трикутника ABC, перетинає сторону AB у точці D, а сторону BC — у точці E. Знайдіть:
1) відрізок BD, якщо AB = 16 см, AC = 20 см, DE = 15 см;
2) відрізок AD, якщо AB = 28 см, BC = 63 см, BE = 27 см.

431. У трикутнику ABC відомо, що AB = 6 см. Через точку M сторони AB проведено пряму, яка паралельна стороні BC і перетинає сторону AC у точці K. Знайдіть невідомі сторони трикутника ABC, якщо AM = 4 см, MK = 8 см, AK = 9 см.

432. Знайдіть висоту вежі (рис. 136), якщо відстані від спостерігача до жердини та до вежі відповідно дорівнюють 1,5 м і 39 м, висота жердини — 3 м, а зріст спостерігача — 1,8 м.

433. Продовження бічних сторін AB і CD трапеції ABCD перетинаються в точці E. Знайдіть відрізок CE, якщо DE = 40 см, BC : AD = 4 : 5.

434. Продовження бічних сторін AB і CD трапеції ABCD перетинаються в точці M. Знайдіть меншу основу трапеції, якщо більша основа AD дорівнює 42 см, AB = 9 см, BM = 54 см

435. Користуючись означенням подібних трикутників, доведіть, що будь-які два рівносторонніх трикутники подібні.

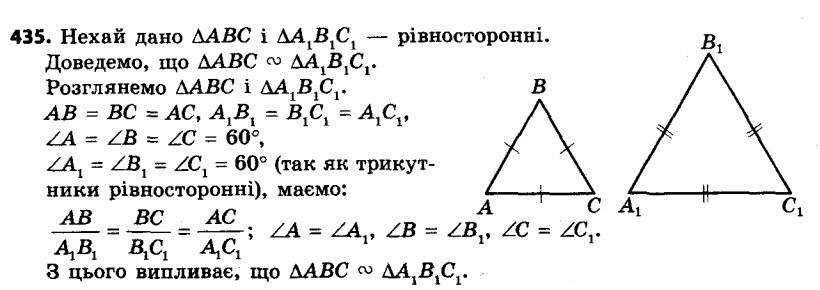
436. Точки M і K — середини сторін CD і AD квадрата ABCD відповідно. Користуючись означенням подібних трикутників, доведіть, що DMDK " DBCD

437. Сторони трикутника відносяться як 5 : 4 : 7. Знайдіть сторони подібного йому трикутника, у якого:
1) периметр дорівнює 64 см;
2) менша сторона дорівнює 24 см.

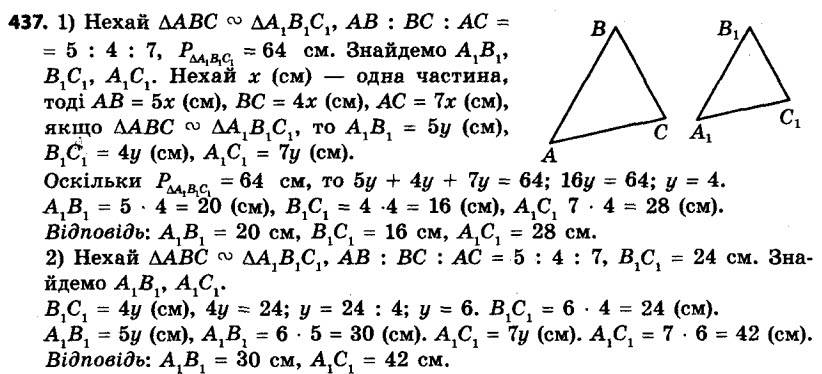438. Сторони даного трикутника дорівнюють 15 см, 25 см і 35 см. Знайдіть сторони подібного йому трикутника, у якого:
1) периметр дорівнює 45 см;
2) різниця найбільшої і найменшої сторін становить 16 см.

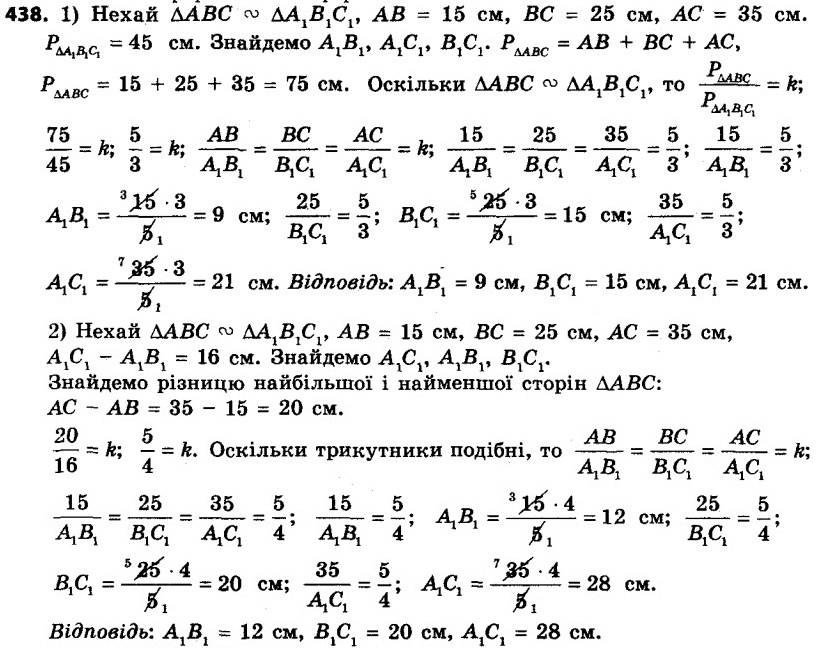439. На рисунку 137 зображено трикутник ABC і вписаний у нього ромб BDEK. Знайдіть сторону ромба, якщо AB = 10 см, BC = 15 см

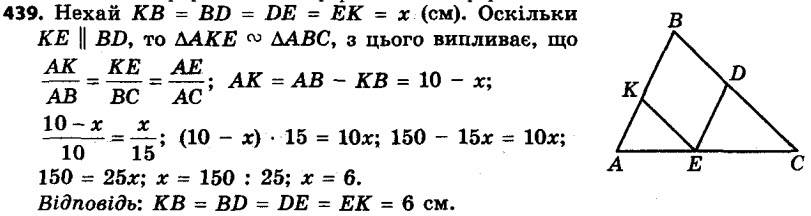440. На рисунку 138 зображено прямокутний трикутник ABC (∠B = 90°) і вписаний у нього квадрат BMKN. Знайдіть відрізок CN, якщо BM = 6 см, AB = 10 см.

441. Два кола із центрами O1 і O2 та радіусами 8 см і 12 см відповідно мають тільки одну спільну точку A (точка А лежить між точками O1 і O2). Їхня спільна зовнішня дотична перетинає пряму O1O2 у точці B. Знайдіть відстані від точки B до центрів даних кіл.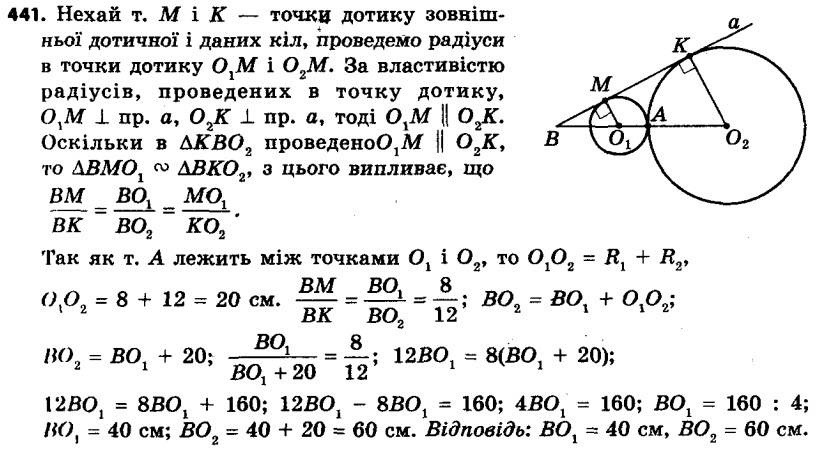

442. Периметр рівнобедреного трикутника дорівнює 48 см. Через середину висоти трикутника, опущеної на його основу, проведено пряму, паралельну бічній стороні. Знайдіть периметр трикутника, який ця пряма відтинає від даного.

443. У рівнобедрений трикутник, основа якого дорівнює 12 см, а бічна сторона — 18 см, вписано коло. Знайдіть відстань між точками дотику цього кола до бічних сторін трикутника.

444. У трикутнику ABC відомо, що AB = 8 см, BC = 12 см, ∠ABC = 120°, BD — бісектриса. Знайдіть відрізок BD.

445. Сторона BC паралелограма ABCD у 2 рази більша за сторону AB. Бісектриси кутів A і B паралелограма перетинають пряму CD у точках M і K відповідно (рис. 139). Знайдіть сторони паралелограма, якщо MK = 18 см.

446. Діагоналі прямокутника ABCD перетинаються в точці O, кут AOD на 60° більший за кут AOB, AC = 24 см. Знайдіть периметр трикутника COD.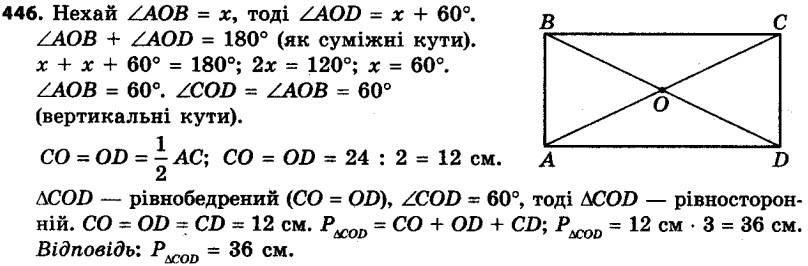

447. Коло, центр якого належить стороні AB трикутника ABC, проходить через точку B, дотикається до сторони AC у точці C і перетинає сторону AB у точці D, причому AD : BD = 1 : 2. Знайдіть кути:
1) трикутника ABC;
2) трикутника BCD.