ГДЗ Геометрія 8 клас. Підручник [Мерзляк А.Г., Полонський В.Б., Якір М.С.] 2021
10. Описане та вписане кола чотирикутника
326. Накресліть прямокутник зі сторонами 2 см і 3 см. Опишіть навколо нього коло.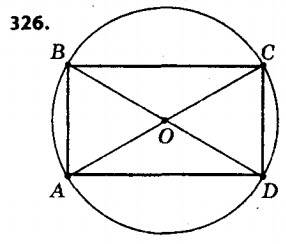
327. Накресліть довільну рівнобічну трапецію. Опишіть навколо неї коло.
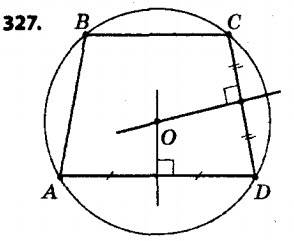 328.° Накресліть рівнобічну трапецію з більшою основою 6 см, бічною стороною 4 см і кутом 60°. Впишіть у неї коло.
328.° Накресліть рівнобічну трапецію з більшою основою 6 см, бічною стороною 4 см і кутом 60°. Впишіть у неї коло.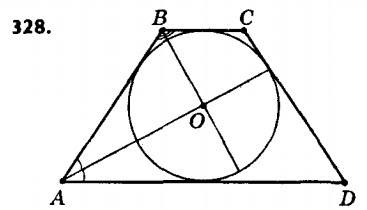 329. Накресліть довільний квадрат. Впишіть у нього коло й опишіть навколо нього коло.
329. Накресліть довільний квадрат. Впишіть у нього коло й опишіть навколо нього коло.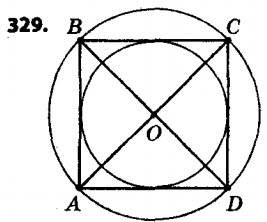 330.° Чи можна описати коло навколо чотирикутника ABCD, якщо його кути A, B, C і D відповідно дорівнюють:
330.° Чи можна описати коло навколо чотирикутника ABCD, якщо його кути A, B, C і D відповідно дорівнюють:1) 90°, 90°, 80°, 100°;
2) 90°, 80°, 90°, 100°;
3) 50°, 70°, 130°, 110°?
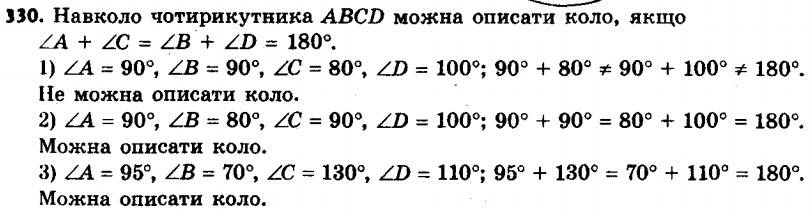 331.° Чи можна описати коло навколо чотирикутника ABCD, якщо його кути A, B, C і D відповідно пропорційні числам:
331.° Чи можна описати коло навколо чотирикутника ABCD, якщо його кути A, B, C і D відповідно пропорційні числам:1) 3, 8, 11, 6;
2) 4, 5, 4, 2?
 332.° Доведіть, що можна описати коло навколо:
332.° Доведіть, що можна описати коло навколо:1) будь-якого прямокутника;
2) будь-якої рівнобічної трапеції.
 333. Яка точка є центром кола, описаного навколо прямокутника?
333. Яка точка є центром кола, описаного навколо прямокутника? 334. Чи можна описати коло навколо ромба, який не є квадратом?
334. Чи можна описати коло навколо ромба, який не є квадратом? 335. У прямокутнику ABCD відомо, що AB = 12 см, ∠CAD = 30°. Знайдіть радіус кола, описаного навколо даного прямокутника.
335. У прямокутнику ABCD відомо, що AB = 12 см, ∠CAD = 30°. Знайдіть радіус кола, описаного навколо даного прямокутника. 336. Чи можна вписати коло в чотирикутник ABCD, якщо його сторони AB, BC, CD, AD відповідно пропорційні числам:
336. Чи можна вписати коло в чотирикутник ABCD, якщо його сторони AB, BC, CD, AD відповідно пропорційні числам:1) 7, 8, 12, 11;
2) 7, 12, 8, 11?
 337. Сума двох протилежних сторін чотирикутника, описаного навколо кола, дорівнює 18 см. Знайдіть периметр даного чотирикутника.
337. Сума двох протилежних сторін чотирикутника, описаного навколо кола, дорівнює 18 см. Знайдіть периметр даного чотирикутника. 338. Бічна сторона рівнобічної трапеції дорівнює 7 см. Чому дорівнює периметр даної трапеції, якщо в неї можна вписати коло?
338. Бічна сторона рівнобічної трапеції дорівнює 7 см. Чому дорівнює периметр даної трапеції, якщо в неї можна вписати коло?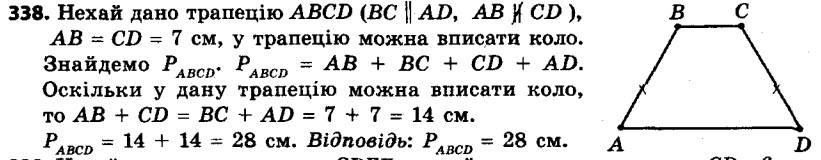 339. У чотирикутнику CDEF, у який можна вписати коло, CD = = 6 см, DE = 8 см, EF = 12 см. Знайдіть сторону CF.
339. У чотирикутнику CDEF, у який можна вписати коло, CD = = 6 см, DE = 8 см, EF = 12 см. Знайдіть сторону CF. 340. Доведіть, що в будь-який ромб можна вписати коло. Яка точка є центром кола, вписаного в ромб?
340. Доведіть, що в будь-який ромб можна вписати коло. Яка точка є центром кола, вписаного в ромб? 341. Чи можна вписати коло в паралелограм, який не є ромбом?
341. Чи можна вписати коло в паралелограм, який не є ромбом? 342. Під яким кутом видно бічну сторону трапеції із центра вписаного кола?
342. Під яким кутом видно бічну сторону трапеції із центра вписаного кола? 343. Один із кутів ромба дорівнює 60°, а більша діагональ — 24 см. Знайдіть радіус кола, вписаного в даний ромб.
343. Один із кутів ромба дорівнює 60°, а більша діагональ — 24 см. Знайдіть радіус кола, вписаного в даний ромб. 344. Доведіть, що коли в прямокутник можна вписати коло, то цей прямокутник є квадратом.
344. Доведіть, що коли в прямокутник можна вписати коло, то цей прямокутник є квадратом. 345. Доведіть, що коли навколо ромба можна описати коло, то цей ромб є квадратом.
345. Доведіть, що коли навколо ромба можна описати коло, то цей ромб є квадратом. 346. Сторона AD чотирикутника ABCD є діаметром кола, описаного навколо нього, ∠ABC = 108°, ∠BCD = 132°. Знайдіть кути BAD, ADC, CAD, BDA.
346. Сторона AD чотирикутника ABCD є діаметром кола, описаного навколо нього, ∠ABC = 108°, ∠BCD = 132°. Знайдіть кути BAD, ADC, CAD, BDA. 347. Знайдіть кути чотирикутника MNKP, вписаного в коло, якщо ∠MKP = 58°, ∠MPN = 34°, ∠KMP = 16°.
347. Знайдіть кути чотирикутника MNKP, вписаного в коло, якщо ∠MKP = 58°, ∠MPN = 34°, ∠KMP = 16°. 348. Рівнобічну трапецію вписано в коло, центр якого належить одній з основ. Кут між діагоналями трапеції, протилежний її бічній стороні, дорівнює 56°. Знайдіть кути трапеції.
348. Рівнобічну трапецію вписано в коло, центр якого належить одній з основ. Кут між діагоналями трапеції, протилежний її бічній стороні, дорівнює 56°. Знайдіть кути трапеції.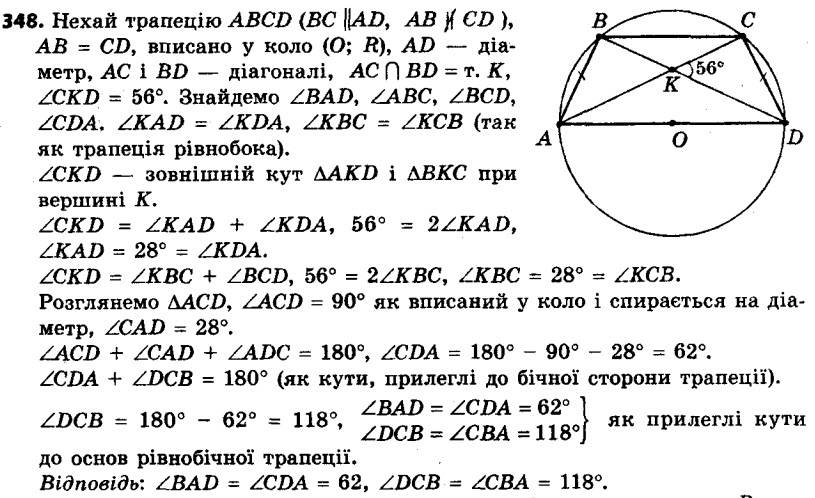 349. Висоти BM і CK гострокутного трикутника ABC перетинаються в точці H. Доведіть, що точки A, K, H і M лежать на одному колі.
349. Висоти BM і CK гострокутного трикутника ABC перетинаються в точці H. Доведіть, що точки A, K, H і M лежать на одному колі. 350. У прямокутну трапецію вписано коло. Точка дотику ділить більшу бічну сторону на відрізки завдовжки 8 см і 50 см. Знайдіть периметр даної трапеції, якщо радіус вписаного кола дорівнює 20 см.
350. У прямокутну трапецію вписано коло. Точка дотику ділить більшу бічну сторону на відрізки завдовжки 8 см і 50 см. Знайдіть периметр даної трапеції, якщо радіус вписаного кола дорівнює 20 см. 351. У прямокутну трапецію вписано коло. Точка дотику ділить більшу бічну сторону на відрізки завдовжки 3 см і 12 см. Знайдіть радіус вписаного кола, якщо периметр трапеції дорівнює 54 см.
351. У прямокутну трапецію вписано коло. Точка дотику ділить більшу бічну сторону на відрізки завдовжки 3 см і 12 см. Знайдіть радіус вписаного кола, якщо периметр трапеції дорівнює 54 см. 352. Центр кола, описаного навколо трапеції, належить більшій основі, а бічна сторона дорівнює меншій основі. Знайдіть кути трапеції.
352. Центр кола, описаного навколо трапеції, належить більшій основі, а бічна сторона дорівнює меншій основі. Знайдіть кути трапеції. 353. Діагональ трапеції, вписаної в коло, дорівнює d. Бічну сторону видно із центра описаного кола під кутом 120°. Знайдіть середню лінію трапеції.
353. Діагональ трапеції, вписаної в коло, дорівнює d. Бічну сторону видно із центра описаного кола під кутом 120°. Знайдіть середню лінію трапеції.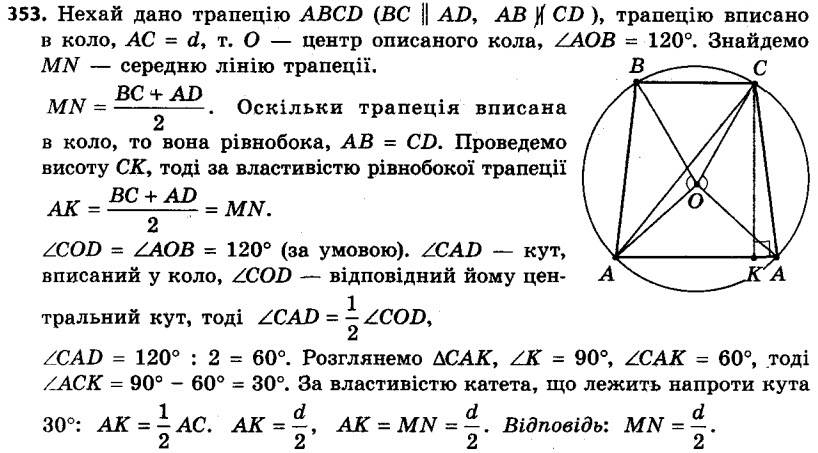 354. Бічні сторони та менша основа рівнобічної трапеції дорівнюють 6 см, а один з її кутів дорівнює 60°. Знайдіть радіус кола, описаного навколо даної трапеції.
354. Бічні сторони та менша основа рівнобічної трапеції дорівнюють 6 см, а один з її кутів дорівнює 60°. Знайдіть радіус кола, описаного навколо даної трапеції. 355. З довільної точки M катета AC прямокутного трикутника ABC опущено перпендикуляр MK на гіпотенузу AB. Доведіть, що ∠MKC = ∠MBC.
355. З довільної точки M катета AC прямокутного трикутника ABC опущено перпендикуляр MK на гіпотенузу AB. Доведіть, що ∠MKC = ∠MBC.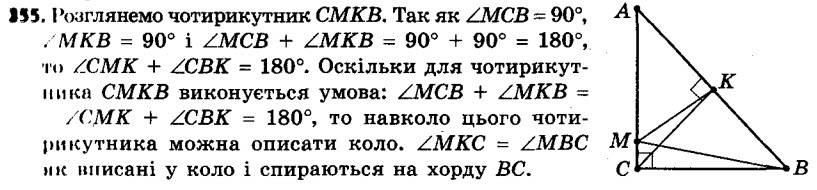 356. З довільної точки O, яка належить гострому куту A, але не належить його сторонам, опущено перпендикуляри OB і OC на його сторони. Доведіть, що ∠OAB = ∠OCB.
356. З довільної точки O, яка належить гострому куту A, але не належить його сторонам, опущено перпендикуляри OB і OC на його сторони. Доведіть, що ∠OAB = ∠OCB. 357. Бісектриси BK і CM трикутника ABC перетинаються в точці O, ∠A = 60°. Знайдіть кут CMK.
357. Бісектриси BK і CM трикутника ABC перетинаються в точці O, ∠A = 60°. Знайдіть кут CMK.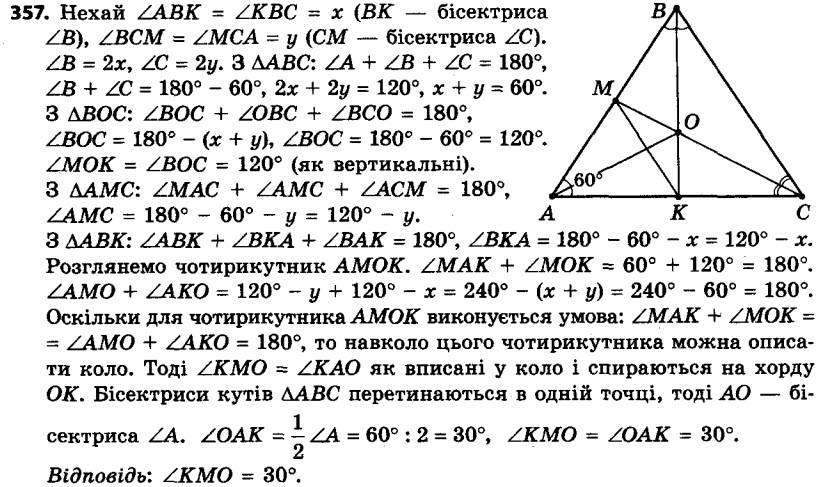 358. Бісектриси MA і KB трикутника MNK перетинаються в точці O, точки A, N, B і O лежать на одному колі. Знайдіть кут N.
358. Бісектриси MA і KB трикутника MNK перетинаються в точці O, точки A, N, B і O лежать на одному колі. Знайдіть кут N.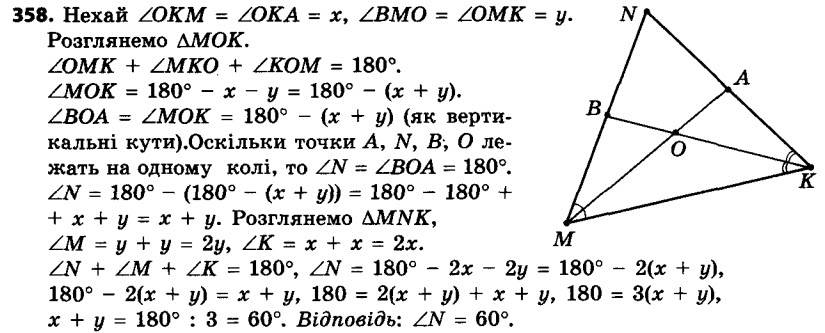 359. Поза прямокутним трикутником ABC на його гіпотенузі AB побудовано квадрат ABFD. Доведіть, що ∠ACO = ∠OCB, де O — точка перетину діагоналей квадрата.
359. Поза прямокутним трикутником ABC на його гіпотенузі AB побудовано квадрат ABFD. Доведіть, що ∠ACO = ∠OCB, де O — точка перетину діагоналей квадрата. 360. Вершини A і B трикутника ABC із прямим кутом C ковзають по сторонах прямого кута з вершиною P (рис. 110). Доведіть, що точка C при цьому переміщується по відрізку.
360. Вершини A і B трикутника ABC із прямим кутом C ковзають по сторонах прямого кута з вершиною P (рис. 110). Доведіть, що точка C при цьому переміщується по відрізку. 361. З довільної точки M, яка належить куту з вершиною A, але не належить його сторонам, проведено перпендикуляри MP і MQ до сторін кута. Із точки A проведено перпендикуляр AK до відрізка PQ. Доведіть, що ∠PAK = ∠MAQ.
361. З довільної точки M, яка належить куту з вершиною A, але не належить його сторонам, проведено перпендикуляри MP і MQ до сторін кута. Із точки A проведено перпендикуляр AK до відрізка PQ. Доведіть, що ∠PAK = ∠MAQ.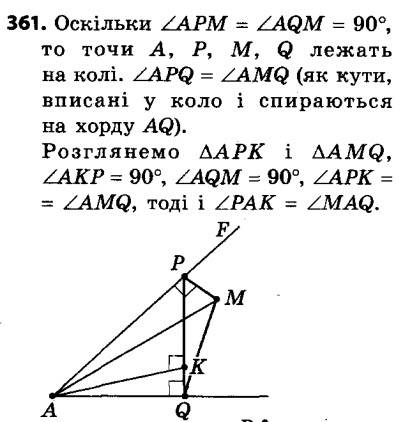
362. У гострокутному трикутнику ABC відрізки CC1 і AA1 — висоти. Доведіть, що серединний перпендикуляр відрізка C1A1 проходить через середину сторони AC.
 363. На бічних сторонах трапеції, у яку можна вписати коло, як на діаметрах побудовано два кола. Доведіть, що ці кола мають одну спільну точку.
363. На бічних сторонах трапеції, у яку можна вписати коло, як на діаметрах побудовано два кола. Доведіть, що ці кола мають одну спільну точку. 364. Через середину діагоналі AC паралелограма ABCD проведено пряму, яка перетинає сторони BC і AD. Ця пряма перетинає прямі AB і CD у точках M і K відповідно. Визначте вид чотирикутника AMCK.
364. Через середину діагоналі AC паралелограма ABCD проведено пряму, яка перетинає сторони BC і AD. Ця пряма перетинає прямі AB і CD у точках M і K відповідно. Визначте вид чотирикутника AMCK. 365. У трикутнику ABC відрізок AD — бісектриса. Через точку D проведено пряму, яка паралельна стороні AC і перетинає сторону AB у точці E. Через точку E проведено пряму, яка паралельна стороні BC і перетинає сторону AC у точці F. Доведіть, що AE = CF.
365. У трикутнику ABC відрізок AD — бісектриса. Через точку D проведено пряму, яка паралельна стороні AC і перетинає сторону AB у точці E. Через точку E проведено пряму, яка паралельна стороні BC і перетинає сторону AC у точці F. Доведіть, що AE = CF.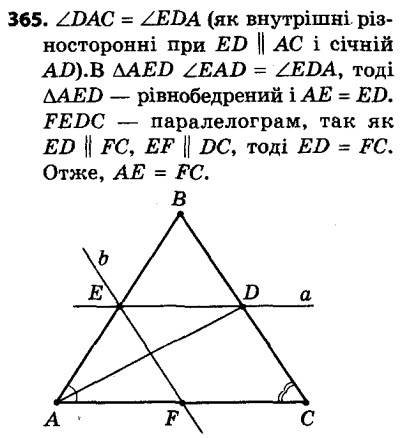 366. Висота BM ромба ABCD, опущена з вершини тупого кута на сторону AD, перетинає діагональ AC у точці K, ∠BKC = 64°. Знайдіть кут ABC.
366. Висота BM ромба ABCD, опущена з вершини тупого кута на сторону AD, перетинає діагональ AC у точці K, ∠BKC = 64°. Знайдіть кут ABC.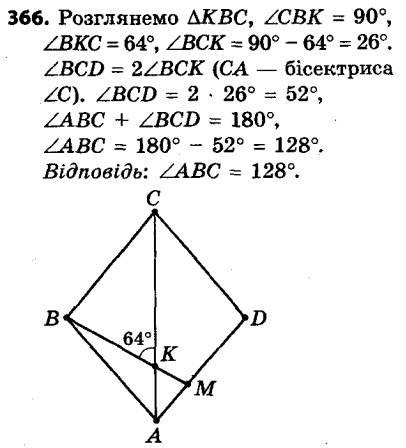 367. Чи можна квадрат розрізати на тисячокутник і 199 п’ятикутників?
367. Чи можна квадрат розрізати на тисячокутник і 199 п’ятикутників?
 ГДЗ 2021 Підручник 8 клас Геометрія Мерзляк Полонський Якір Гімназія
ГДЗ 2021 Підручник 8 клас Геометрія Мерзляк Полонський Якір Гімназія
 Якщо помітили в тексті помилку, виділіть її та натисніть Ctrl + Enter
Якщо помітили в тексті помилку, виділіть її та натисніть Ctrl + Enter 15.10.2021,
15.10.2021,
 31 565,
31 565,
 0
0
 Назад
Назад




![ГДЗ Природознавство 5 клас. Підручник [Ярошенко О.Г., Бойко В.М.] 2018 ГДЗ Природознавство 5 клас. Підручник [Ярошенко О.Г., Бойко В.М.] 2018](/uploads/posts/2019-04/1555779316_5_p_y_u2018.jpg)
![ГДЗ Основи правознавства 9 клас. Підручник [Наровлянський О. Д.] 2017 ГДЗ Основи правознавства 9 клас. Підручник [Наровлянський О. Д.] 2017](/uploads/posts/2019-02/1550928122_9k_p_n_2017.jpg)
![ГДЗ Українська мова 8 клас. Підручник [Глазова О.П.] 2021 ГДЗ Українська мова 8 клас. Підручник [Глазова О.П.] 2021](/uploads/posts/2021-10/1633720388_8k_y_g_2021.jpg)
![ГДЗ Вступ до історії 5 клас. Підручник [Гісем О.В.] 2018 ГДЗ Вступ до історії 5 клас. Підручник [Гісем О.В.] 2018](/uploads/posts/2019-07/1564163269_5k_i_h_2018.jpg)