ГДЗ Геометрія 8 клас. Підручник [Мерзляк А.Г., Полонський В.Б., Якір М.С.] 2021

489. На одній стороні кута A відкладено відрізки AB і AD, а на другій — відрізки AC і AE. Чи подібні трикутники ABC і ADE, якщо AB = 4 см, AD = 20 см, AC = 10 см, AE = 8 см?
490. На сторонах AB і AC трикутника ABC (рис. 163) позначили відповідно точки D і E так, що AD = 4/7 AC, AE = 4/7 AB. Знайдіть відрізок DE, якщо BC = 21 см.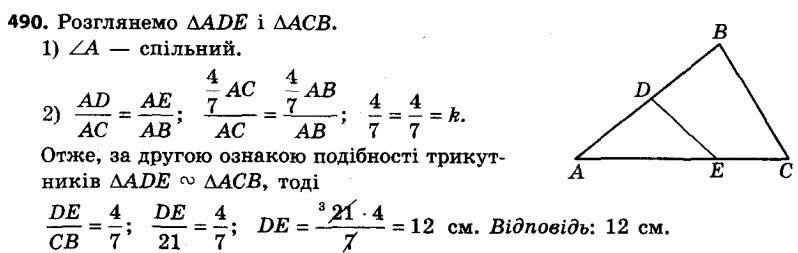
491. У трикутнику ABC відомо, що AB = 21 см, AC = 42 см, BC = 28 см (рис. 164). На продовженнях відрізків AB і BC за точку B відкладено відповідно відрізки BM і BK, BM = 8 см, BK = 6 см. Знайдіть відрізок KM.
492. Відрізки AB і CD перетинаються в точці O (рис. 165), AO = 24 см, BO = 16 см, CO = 15 см, OD = 10 см, ∠ACO = 72°. Знайдіть кут BDO
493. На сторонах AC і BС трикутника ABC позначили відповідно точки M і K так, що CM = 15 см, CK = 12 см. Знайдіть відрізок MK, якщо AC = 20 см, BC = 25 см, AB = 30 см.
494. Чи подібні трикутники ABC і A1B1C1, якщо:
1) AB = 6 см, BC = 10 см, AC = 14 см, A1B1 = 9 см, B1C1 = 15 см, A1C1 = 21 см;
2) AB = 1,3 см, BC = 2,5 см, AC = 3,2 см, A1B1 = 26 см, B1C1 = 50 см, A1C1 = 60 см?
495. Чи подібні два трикутники, якщо сторони одного відносяться як 3 : 8 : 9, а сторони другого дорівнюють 24 см, 9 см, 27 см?
496. У трикутниках ABC і A1B1C1 відомо, що ∠A = ∠A1, кожна зі сторін AB і AC становить 0,6 сторін A1B1 і A1C1 відповідно. Знайдіть сторони BC і B1C1, якщо їхня сума дорівнює 48 см.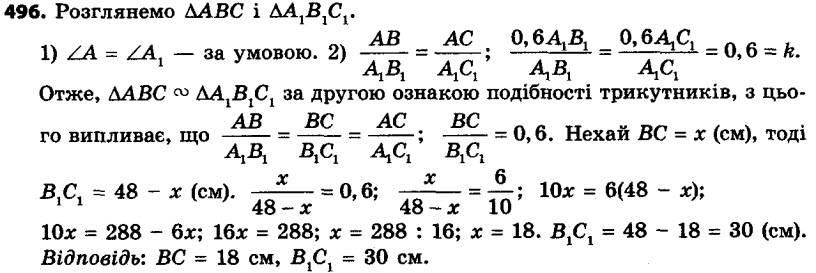
497. У трикутниках DEF і MKN відомо, що ∠E = ∠K, а кожна зі сторін DE і EF у 2,5 раза більша за сторони MK і KN відповідно. Знайдіть сторони DF і MN, якщо їхня різниця дорівнює 30 см.
498. На сторонах AB і AC трикутника ABC позначили відповідно точки D і E так, що AD : DB = AE : EC = 3 : 5. Знайдіть відрізок DE, якщо BC = 16 см.
499. З дерев’яних паличок виготовили три подібні різносторонні трикутники. У кожному з них більшу сторону пофарбували в блакитний колір, а меншу — у жовтий. З блакитних паличок склали один трикутник, а з жовтих — другий. Чи будуть ці трикутники подібні?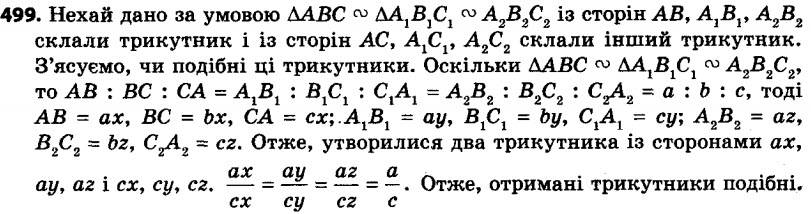
500. У трикутнику ABC відомо, що AC = a, AB = BC = b, AM і CK — бісектриси трикутника. Знайдіть відрізок MK.
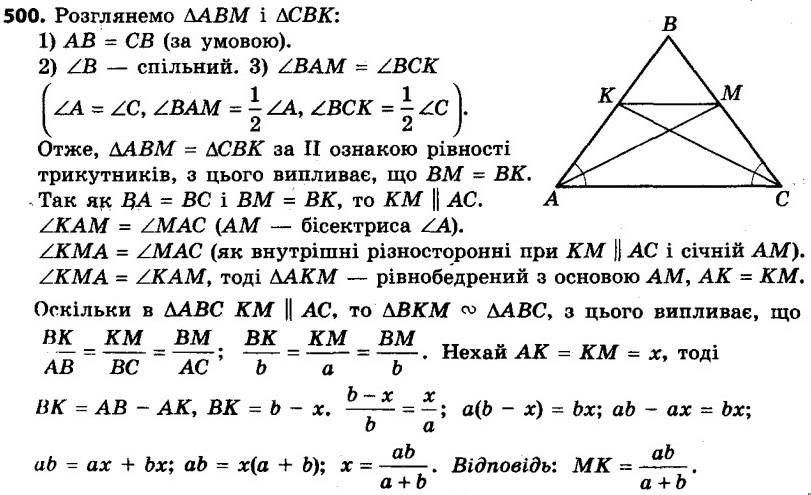501. У трикутнику ABC відомо, що AB = 8 см, BC = 12 см, AC = = 16 см. На стороні AC позначено точку D так, що CD = 9 см. Знайдіть відрізок BD.
502. Із точки A проведено два промені AM і AN. На промені AM позначено точки H і B, а на промені AN — точки C і D так, що AHæAB = ACæAD. Доведіть, що точки H, B, C і D лежать на одному колі.
503. На медіані BM трикутника ABC позначили точку K так, що ∠MKC = ∠BCM. Доведіть, що ∠AKM = ∠BAM.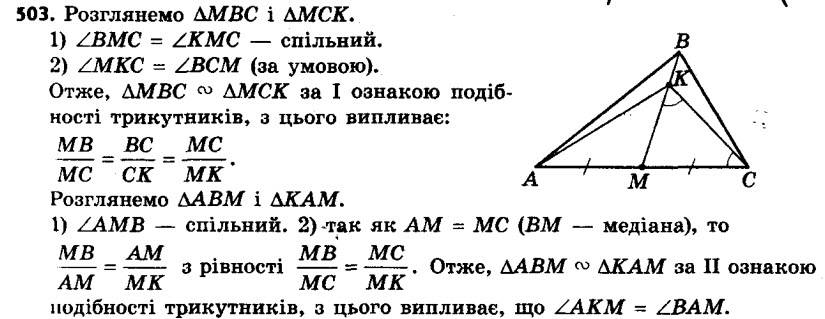
504. Відрізки AB і CD перетинаються в точці M. Відомо, що AMæMB = CMæMD. Доведіть, що точки A, B, C і D лежать на одному колі.
505. На спільній хорді двох кіл, що перетинаються, позначили точку M і через неї провели хорди AB і CD (рис. 166). Доведіть, що ∠DAB = ∠BCD.
506. Периметр паралелограма ABCD дорівнює 46 см, ∠BAD = ∠ADB. Знайдіть сторони паралелограма, якщо периметр трикутника BCD дорівнює 32 см.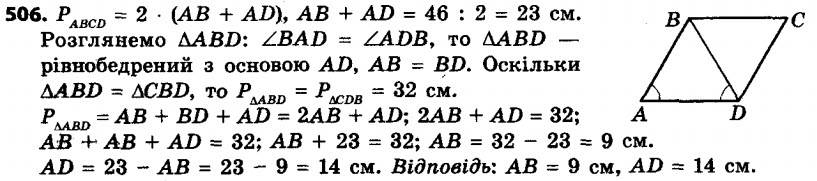
507. На діагоналі BD квадрата ABCD позначили точку E так, що DE = AD. Через точку E проведено пряму, яка перпендикулярна до прямої BD і перетинає сторону AB у точці F. Доведіть, що AF = FE = BE.
508. У трапеції ABCD відомо, що ∠B = 90°, ∠C = 150°, BC = 5 см. Знайдіть сторону CD, якщо висота трапеції, проведена з вершини C, розбиває дану трапецію на трикутник і квадрат.

---

---

Назад

Вперед

1 ... 11 12 13 14 15 16 17 18 19 ... 32

ГДЗ 2021 Підручник 8 клас Геометрія Мерзляк Полонський Якір Гімназія