ГДЗ Геометрія 8 клас. Підручник [Мерзляк А.Г., Полонський В.Б., Якір М.С.] 2021

579. Побудуйте кут:
1) тангенс якого дорівнює 4/5;
2) синус якого дорівнює 2/3 .
580. Побудуйте кут:
1) косинус якого дорівнює 1/4;
2) тангенс якого дорівнює 1/2 .
581. Катет і гіпотенуза прямокутного трикутника відповідно дорівнюють 8 см і 10 см. Знайдіть:
1) синус кута, який лежить проти меншого катета;
2) косинус кута, який прилягає до більшого катета;
3) тангенс кута, протилежного меншому катету.
582. Катети прямокутного трикутника дорівнюють 3 см і 2 см. Знайдіть:
1) тангенс кута, прилеглого до більшого катета;
2) синус кута, протилежного меншому катету;
3) косинус кута, прилеглого до більшого катета.
583. Знайдіть значення виразу:
1) cos2 45° + tg2 60°;
2) 2 cos2 60° – sin2 30° + sin 60° tg 30°.

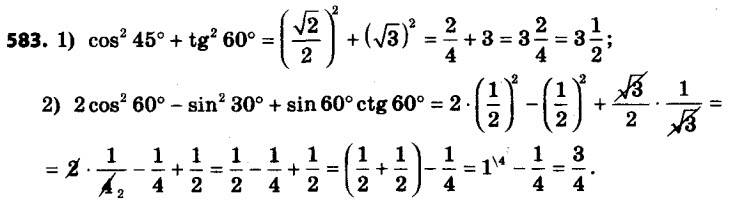
584. Знайдіть значення виразу:
1) cos2 30° – sin2 45°;
2) 3 tg2 30° + 4 tg 45° + cos 30° tg 60°.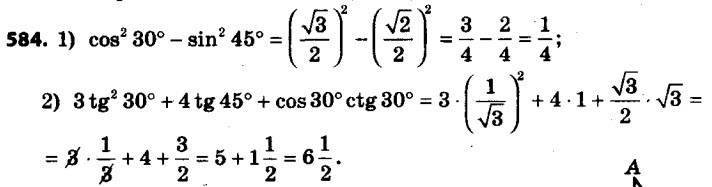585. У трикутнику ABC відомо, що ∠C = 90°, BC = 77 см, AB = 125 см. Знайдіть синуси гострих кутів трикутника.
586. У трикутнику ABC відомо, що ∠C = 90°, BC = 41 см, AC = 20 см. Знайдіть косинуси гострих кутів трикутника.
587. Знайдіть sin a і tg a, якщо cos 1/3.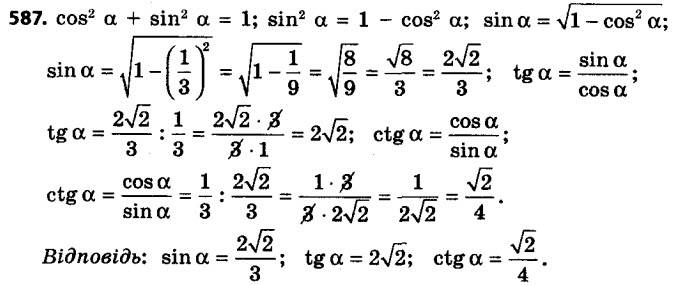
588. Знайдіть cos b і tg b, якщо sin 4/5.
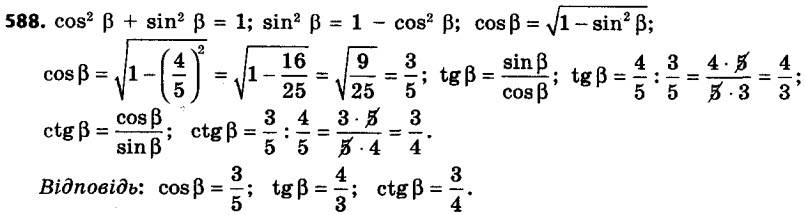589. Синус гострого кута прямокутного трикутника дорівнює. Знайдіть синус, косинус і тангенс другого гострого кута цього трикутника.
590. Основа рівнобедреного трикутника дорівнює 24 см, а бічна сторона — 13 см. Знайдіть синус, косинус і тангенс кута між бічною стороною трикутника та висотою, проведеною до його основи.
591. Бічна сторона рівнобедреного трикутника дорівнює 17 см, а висота, проведена до основи, — 8 см. Знайдіть синус, косинус і тангенс кута при основі трикутника.
592.• Знайдіть кути ромба, діагоналі якого дорівнюють 4 см.
593. Знайдіть кути між діагоналлю прямокутника та його сторонами, довжини яких дорівнюють 3 см.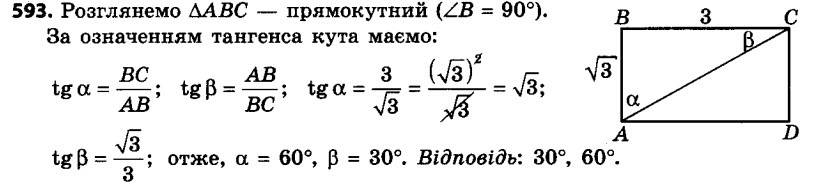
594. У трапеції ABCD відомо, що AB = CD = 9 см, BC = 10 см, AD = 14 см. Знайдіть синус, косинус і тангенс кута A трапеції.
595. У прямокутній трапеції ABCD відомо, що BC || AD, ∠A = 90°, AB = 4 см, BC = 8 см, AD = 12 см. Знайдіть кути трапеції.
596. Доведіть, що тангенси гострих кутів прямокутного трикутника є взаємно оберненими числами.
597. Доведіть тотожність.
598. Знайдіть значення виразу:
1) sin2 18° + sin2 72°;
2) cos3 36° – sin3 54°.
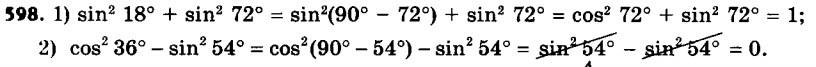599. Катети прямокутного трикутника дорівнюють 30 см і 40 см. Знайдіть синус, косинус і тангенс кута між медіаною та висотою, проведеними до гіпотенузи.
600. У трикутнику ABC відомо, що AB = BC, BD і AM — висоти трикутника, BD : AM = = 3 : 1. Знайдіть cos C.
601. У трикутнику ABC відомо, що AB = BC, BD і CK — висоти трикутника, cos A = = 3 7 . Знайдіть відношення CK : BD.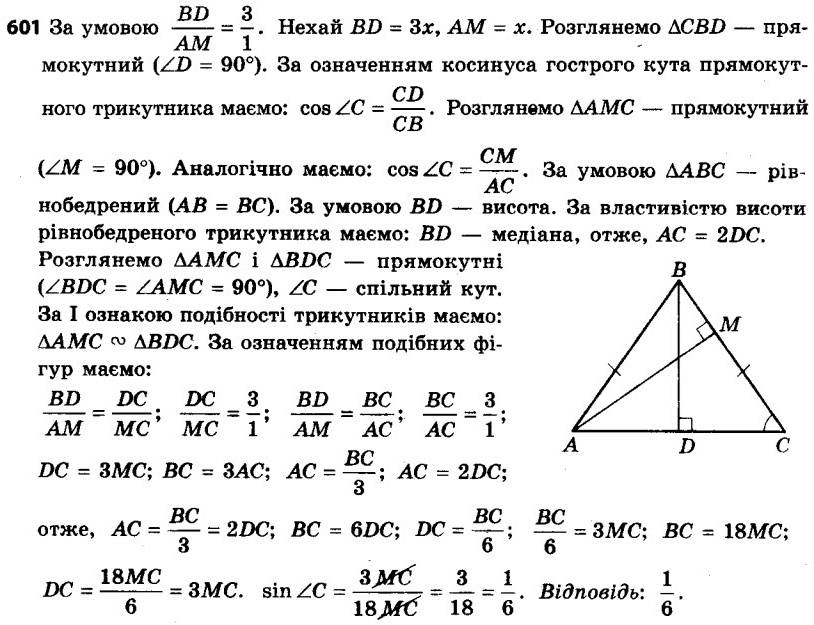
602. Доведіть, що кути ABC і DEF, зображені на рисунку 184, рівні.
603. Бісектриси кутів A і B паралелограма ABCD перетинаються в точці M, AB = 6 см. Знайдіть радіус кола, яке проходить через точки A, B і M.
604. Хорди AB і BC кола перпендикулярні, а відстань між їхніми серединами дорівнює 12 см. Знайдіть радіус кола.

605. У трикутнику ABC відомо, що BK — висота, AM — бісектриса, BK = 26 см, AB : AC = 6 : 7. Із точки M опущено перпендикуляр MD на сторону AC. Знайдіть відрізок MD.606. Дано два круги, які не мають спільних точок. Чи існує точка, що не належить жодному з кругів, така, що будь-яка пряма, яка проходить через цю точку, перетинає хоча б один із цих кругів?

---

---

Назад

Вперед

1 ... 14 15 16 17 18 19 20 21 22 ... 32

ГДЗ 2021 Підручник 8 клас Геометрія Мерзляк Полонський Якір Гімназія