ГДЗ Геометрія 8 клас. Підручник [Мерзляк А.Г., Полонський В.Б., Якір М.С.] 2021

111. Накресліть прямокутник. Користуючись лише лінійкою, знайдіть точку, яка рівновіддалена від його вершин.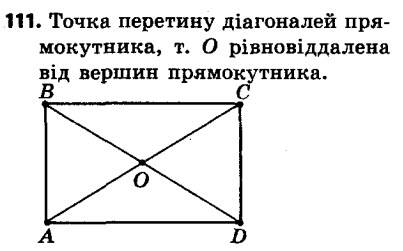
112. Доведіть, що чотирикутник, усі кути якого прямі, є прямокутником.
113. Діагоналі прямокутника ABCD (рис. 46) перетинаються в точці O. Доведіть, що трикутники AOB і AOD рівнобедрені.
114. Діагоналі прямокутника ABCD (рис. 46) перетинаються в точці O, ∠ABD = 64°. Знайдіть кути COD і AOD.
115. Діагоналі прямокутника ABCD (рис. 46) перетинаються в точці O, ∠ADB = 30°, BD = 10 см. Знайдіть периметр трикутника AOB.
116. Кут між діагоналями прямокутника дорівнює 60°, а менша сторона прямокутника дорівнює 8 см. Знайдіть діагональ прямокутника.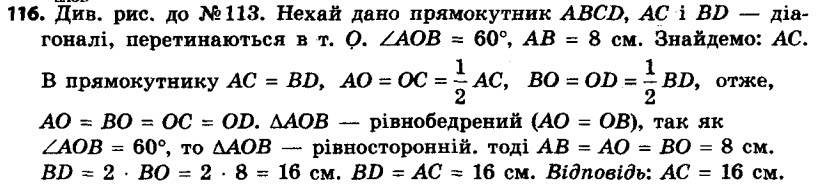
117. На діагоналі AC прямокутника ABCD відкладено рівні відрізки AM і CK (точка M лежить між точками A і K). Доведіть, що чотирикутник BKDM — паралелограм, відмінний від прямокутника.
118. На продовженні діагоналі BD прямокутника ABCD за точку B позначили точку E, а на продовженні за точку D — точку F так, що BE = DF. Доведіть, що чотирикутник AECF — паралелограм, відмінний від прямокутника.
119. Точка M — середина сторони BC прямокутника ABCD, MA ^ MD, периметр прямокутника дорівнює 36 см. Знайдіть сторони прямокутника.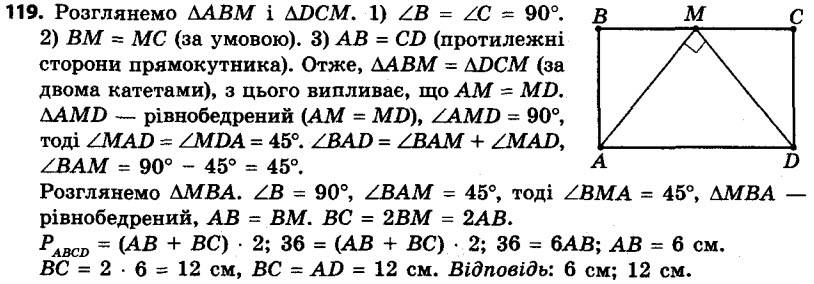
120. Периметр прямокутника ABCD дорівнює 30 см. Бісектриси кутів A і D перетинаються в точці M, яка належить стороні BC. Знайдіть сторони прямокутника
121. Гіпотенуза рівнобедреного прямокутного трикутника дорівнює 55 см. Прямокутник ABCD побудовано так, що дві його вершини A і D належать гіпотенузі, а дві інші — катетам даного трикутника. Знайдіть сторони прямокутника, якщо AB : BC = 3 : 5
122. У трикутнику ABC відомо, що ∠C = 90°, AC = BC = 6 см. Прямокутник CMKN побудовано так, що точка M належить катету AC, точка N — катету BC, а точка K — гіпотенузі AB. Знайдіть периметр прямокутника CMKN.
123. Доведіть, що коли діагоналі паралелограма утворюють рівні кути з однією з його сторін, то цей паралелограм є прямокутником
124. Доведіть, що медіана прямокутного трикутника, проведена до гіпотенузи, дорівнює її половині.
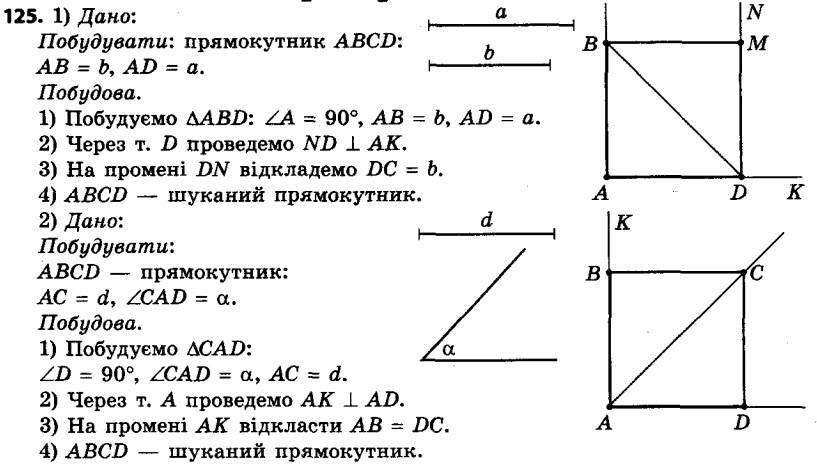
125. Побудуйте прямокутник:
1) за двома сторонами;
2) за діагоналлю та кутом між діагоналлю та стороною.
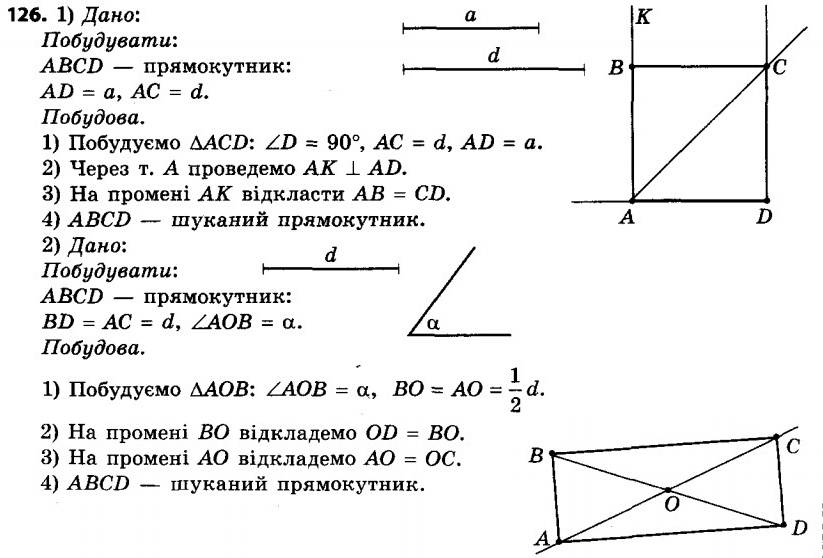
126. Побудуйте прямокутник:
1) за стороною та діагоналлю;
2) за діагоналлю та кутом між діагоналями.
127. Серединний перпендикуляр діагоналі AC прямокутника ABCD перетинає сторону BC у точці M так, що BM : MC = 1 : 2. Знайдіть кути, на які діагональ прямокутника ділить його кут.
128. У прямокутнику ABCD відомо, що ∠BCA : ∠DCA = 1 : 5, AC = 18 см. Знайдіть відстань від точки C до діагоналі BD.
129. Доведіть, що бісектриси кутів паралелограма, у якого сусідні сторони не рівні, перетинаючись, утворюють прямокутник.
130. Побудуйте прямокутник за стороною та кутом між діагоналями, який протилежний даній стороні.
131. Побудуйте прямокутник:
1) за діагоналлю та різницею двох сторін;
2) за периметром і діагоналлю;
3) за периметром і кутом між діагоналями.
132. У трикутнику ABC відомо, що ∠C = 48°, відрізки AK і BM — його висоти. Знайдіть кут між прямими AK і BM.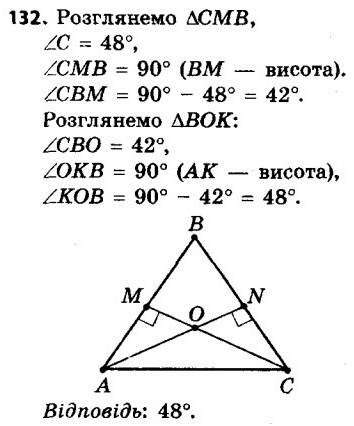
133. На стороні AC трикутника ABC позначено точку D так, що ∠A = ∠CBD. Знайдіть кут ABC, якщо трикутники ABD і BCD мають ще одну пару рівних кутів.
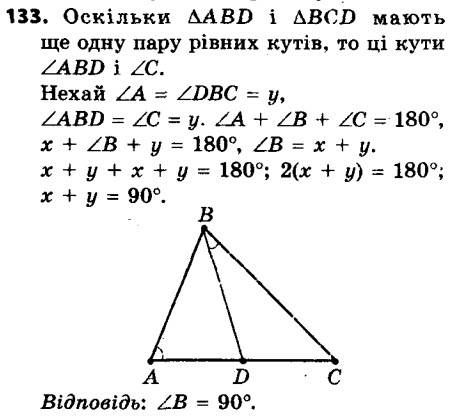134. Відрізок AD — бісектриса трикутника ABC. Через точку C проведено пряму, яка паралельна прямій AD і перетинає пряму AB у точці E. Визначте вид трикутника ACE.
135. На площині позначено 1000 точок. Доведіть, що існує пряма, відносно якої у кожній півплощині лежать по 500 точок.

---

---

Назад

Вперед

1 2 3 4 5 6 7 8 9 10 ... 32

ГДЗ 2021 Підручник 8 клас Геометрія Мерзляк Полонський Якір Гімназія